facits trippelintegral tar bort parametrar

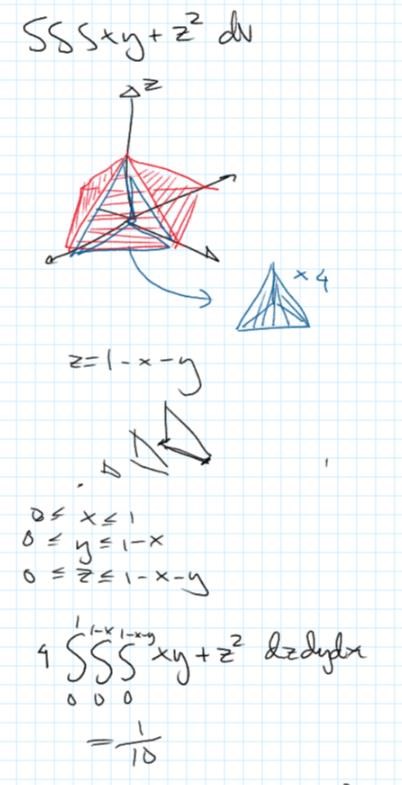
Det ska bli rätt även om man har kvar xy, ja. 

Kan du visa stegen i din integrering? 

jag gjorde det på datorn. men om du säger att min tankegång är rätt så är det säkert bara ett slarvfel. tack :)

Jag menade bara att man kan ha kvar xy. Jag har inte kollat dina integrationsgränser. 

skillnaden till mitt o facits integrationsgärnser är att jag har bytt ut z till x

solaris skrev:

skillnaden till mitt o facits integrationsgärnser är att jag har bytt ut z till x

Varför har du gjort det?

solaris skrev:

skillnaden till mitt o facits integrationsgärnser är att jag har bytt ut z till x

Det gör ingen skillnad; området är symmetriskt, så det går lika bra att räkna med $z$ först.

Däremot har Laguna fel. Du får faktiskt inte ha kvar $xy$-termen om du enbart skall integrera över en fjärdedel av området. Det faktum att man kan integrera på en fjärdedel av området bygger nämligen på att funktionen är jämn relativt $x$ och $y$. Detta gäller enbart funktionen $f(x,y,z)=z^2$, inte $f(x,y,z)=xy+z^2$.

Lite mer ordentligt kan vi säga att vi börjar med att dela upp integralen enligt:

$\displaystyle\iiint_R xy+z^2\ dxdydz=\iiint_R xy\ dxdydz+\iiint_R z^2\ dxdydz=$

På den vänstra integralen inser vi att integranden $f(x,y,z)=xy$ är udda i $x$-led, d.v.s. $f(-x,y,z)=-f(x,y,z)$. Tillsammans med det faktum att området är symmetriskt i $x$-led gör detta att integralen blir lika med noll.

På den högra integralen ser vi att integranden $f(x,y,z)=z^2$ är jämn i $x$-led, d.v.s. $f(-x,y,z)=f(x,y,z)$. Eftersom området är symmetriskt i $x$-led ger detta att vi kan beräkna integralen enbart där $x\geq0$ och sedan dubbla resultatet:

$=\displaystyle\iiint_R z^2\ dxdydz=2\displaystyle\iiint_{R_{x\geq0}}z^2\ dxdydz=$

Vidare ser vi även att integranden är jämn i $y$-led, d.v.s. $f(x,-y,z)=f(x,y,z)$. Då området är symmetriskt i $y$-led ger detta att integralen kan beräknas i delen av området där $y\geq0$ och sedan dubbla. Detta resulterar i att vi endast behöver integrera i första oktanten:

$=4\displaystyle\iiint_{R_{x,y\geq0}}z^2\ dxdydz$

Observera dock att denna förenkling endast gällde för att funktionen var jämn i $x$- och $y$-led. Om vi sparar $xy$-termen gäller inte detta, och vi får då inte integrera i första oktanten och multiplicera med fyra.

Ja, jag hade fel. Jag tänkte inte efter.