Faktorisera x^8+16

Ledning:

Om A*B = 0 så är antingen A=0, eller så är B=0

Utnyttja detta för att dela upp problemet i delproblem. Hur många lösningar (rötter) förväntar du dig?

Får du använda de Moivres formel?

I så fall kan du enkelt hitta nollställena och därmed faktorerna. De kommer att förekomma i komplexkonjugerade par

Sedan kan du multiplicera ihop dessa faktorer parvis precis som du skriver, för att få polynom med enbart reella koefficienter.

Tack!

Då ska jag alltså lösa (x^4-4i) = 0 och (x^4+4i) = 0 ?

Jag förväntar mig 8 lösningar eftersom vi har 8 i exponenten i polynomet x^8+16, men jag kanske har fel?

När det gäller antalet reella faktorer som jag kan faktorisera polynomet till, så ska det nog bli 4 faktorer.

Ja, jag kan använda De Moivres formel.

Bör jag då utgå från x^8+16 eller ska jag applicera De Moivres formel på x^4-4i respektive  x^4+4i ?

Kanelbullen skrev:

Ja, jag kan använda De Moivres formel.

Bör jag då utgå från x^8+16 eller ska jag applicera De Moivres formel på x^4-4i respektive  x^4+4i ?

Det första, dvs lös ekvationen x^8 + 16 = 0.

Jag finner de 8 lösningarna till $x^8=-16$ med hjälp av de Moivres formel.

Talet $-16$ skrivs på polär form 

$16\left(\cos \right(\frac{3\mathrm{\pi }}{2})+i\sin (\frac{3\mathrm{\pi }}{2}\left)\right).$

Antag att $x=r\left(\cos \right(v)+i\sin (v\left)\right)$, då är $x^8=r^8\left(\cos \right(8v)+i\sin (8v\left)\right).$

Absolutbeloppet ges av $r^8=\left|16\right|\iff \mathit{r}\mathbf{=}\sqrt[\mathbf{8}]{\mathbf{16}}.$

Argumentet ges av $8v=\frac{3\mathrm{\pi }}{2}\iff v=\frac{3\mathrm{\pi }}{2}/8=\frac{3\mathrm{\pi }}{2}·\frac{1}{8}=\frac{\mathbf{3}\mathbf{\pi }}{\mathbf{16}}.$

Man ska även lägga till ett varv $\frac{2n\mathrm{\pi }}{8}=\frac{\mathbf{4}\mathbf{n}\mathbf{\pi }}{\mathbf{16}}.$

Samtliga lösningar ges av $\frac{\mathbf{3}\mathbf{\pi }}{\mathbf{16}}\mathbf{+}\frac{\mathbf{4}\mathbf{n}\mathbf{\pi }}{\mathbf{16}}$ för $\mathbf{0}\mathbf{\le }\mathit{n}\mathbf{\le }\mathbf{7}.$

Jag kommer att visa mina lösningar i nästa inlägg jag gör och därefter multiplicera ihop de konjugerade paren för att få fyra reella faktorer.

Kanelbullen skrev:

Jag finner de 8 lösningarna till $x^8=-16$ med hjälp av de Moivres formel.

Talet $-16$ skrivs på polär form 

$16\left(\cos \right(\frac{3\mathrm{\pi }}{2})+i\sin (\frac{3\mathrm{\pi }}{2}\left)\right).$

[...]

Du blandar ihop realdel och imaginärdel här i början. Argumentet $\frac{3\pi}{2}$ ger ett rent imaginärt tal.

Har du verkligen markerat talet -16 i det komplexa talplanet? Om inte så kan det vara förklaringen till felet.

Det har du alldeles rätt i Yngve. Jag har väl uttryckt $-16i$ på polär form ovan?

Talet $-16$ skrivs på polär form 

$16\left(\cos \right(\mathrm{\pi })+i\sin (\mathrm{\pi }\left)\right).$

De 8 lösningarna ska då gälla för $\frac{\mathbf{\pi }}{\mathbf{8}}\mathbf{+}\frac{\mathbf{2}\mathbf{n}\mathbf{\pi }}{\mathbf{8}}$ för $\mathbf{0}\mathbf{\le }\mathit{n}\mathbf{\le }\mathbf{7}\mathbf{.}$

n = 0 ger $\sqrt[8]{16}\left(\cos \right(\frac{\mathrm{\pi }}{8})+i\sin (\frac{\mathrm{\pi }}{8}\left)\right).$

n = 1 ger $\sqrt[8]{16}\left(\cos \right(\frac{3\mathrm{\pi }}{8})+i\sin (\frac{3\mathrm{\pi }}{8}\left)\right).$

n = 2 ger $\sqrt[8]{16}\left(\cos \right(\frac{5\mathrm{\pi }}{8})+i\sin (\frac{5\mathrm{\pi }}{8}\left)\right).$

n = 3 ger $\sqrt[8]{16}\left(\cos \right(\frac{7\mathrm{\pi }}{8})+i\sin (\frac{7\mathrm{\pi }}{8}\left)\right).$

n = 4 ger $\sqrt[8]{16}\left(\cos \right(\frac{9\mathrm{\pi }}{8})+i\sin (\frac{9\mathrm{\pi }}{8}\left)\right).$

n = 5 ger $\sqrt[8]{16}\left(\cos \right(\frac{11\mathrm{\pi }}{8})+i\sin (\frac{11\mathrm{\pi }}{8}\left)\right).$

n = 6 ger $\sqrt[8]{16}\left(\cos \right(\frac{13\mathrm{\pi }}{8})+i\sin (\frac{\mathrm{\pi }}{8}\left)\right).$

n = 7 ger $\sqrt[8]{16}\left(\cos \right(\frac{15\mathrm{\pi }}{8})+i\sin (\frac{15\mathrm{\pi }}{8}\left)\right).$

Nu ska jag hitta de konjugerade paren av rötter och multiplicera dem. Hur finner jag dem som hör ihop?

Räkneregeln för multiplikation av komplexa tal på polär form är att man multiplicerar absolutbeloppen och adderar argumenten.

Kanelbullen skrev:

[...]

Nu ska jag hitta de konjugerade paren av rötter och multiplicera dem. Hur finner jag dem som hör ihop?

[...]

Rita en cirkel runt origo i det komplexa talplanet. Ange cirkelns radie till $\sqrt{2}$.

Rita in de 8 komplexa talen, de ligger jämnt fördelade på cirkeln.

Då är det lätt att se vilka komplexkonjugerade par som hör ihop. Det är de par som har samma realdel (dvs x-värden) men vars imaginärdelar (dvs y-värden) har omvända tecken.

Visa din bild.

Absolutbeloppet är $\sqrt[8]{16} = \sqrt{2}$ och när jag ritar upp de 8 lösningarna i det komplexa talplanet är därför  radien $\sqrt{2}.$

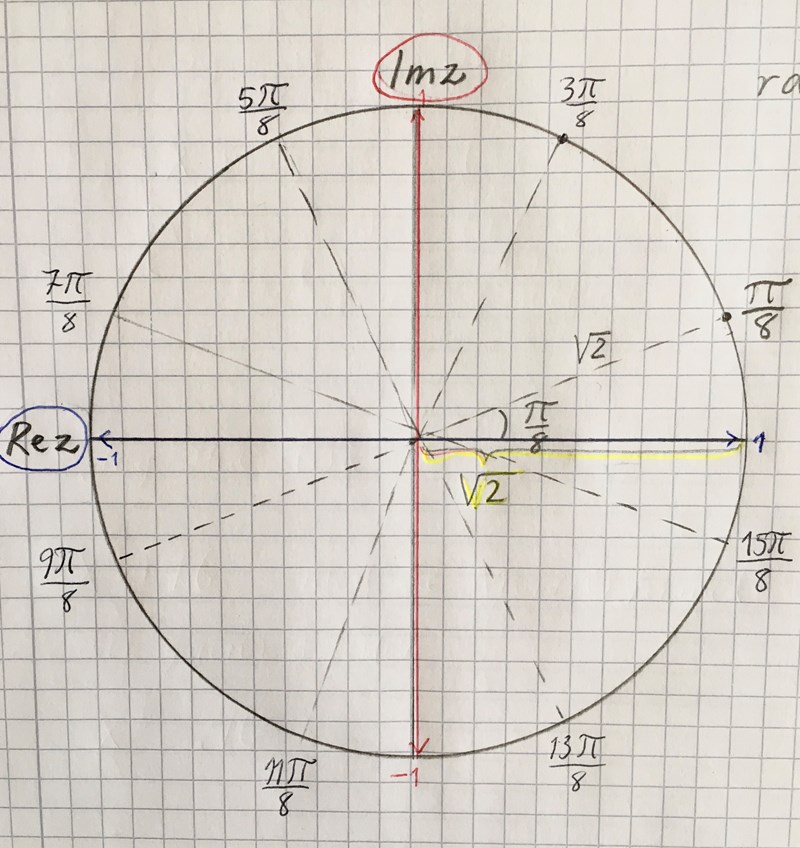
Nu kan jag se vilka par av rötter som är konjugerade och som hör ihop. De står mitt emot varandra i cirkeln.

Vinklarna som ska ses som konjugerade par är:

$$\begin{gathered} \frac{\mathrm{\pi }}{8}, \frac{9\mathrm{\pi }}{8} \\ \frac{3\mathrm{\pi }}{8},\frac{11\mathrm{\pi }}{8} \\ \frac{5\mathrm{\pi }}{8},\frac{13\mathrm{\pi }}{8} \\ \frac{7\mathrm{\pi }}{8},\frac{15\mathrm{\pi }}{8} \end{gathered}$$

Avståndet mellan dem i enhetscirkeln är $\mathrm{\pi },$ dvs. ett halvt varv.

Kanelbullen skrev:

Absolutbeloppet är $\sqrt[8]{16} = \sqrt{2}$ och när jag ritar upp de 8 lösningarna i det komplexa talplanet är därför  radien $\sqrt{2}.$

Nu kan jag se vilka par av rötter som är konjugerade och som hör ihop. De står mitt emot varandra i cirkeln.

Vinklarna som ska ses som konjugerade par är:

$$\begin{gathered} \frac{\mathrm{\pi }}{8}, \frac{9\mathrm{\pi }}{8} \\ \frac{3\mathrm{\pi }}{8},\frac{11\mathrm{\pi }}{8} \\ \frac{5\mathrm{\pi }}{8},\frac{13\mathrm{\pi }}{8} \\ \frac{7\mathrm{\pi }}{8},\frac{15\mathrm{\pi }}{8} \end{gathered}$$

Avståndet mellan dem i enhetscirkeln är $\mathrm{\pi },$ dvs. ett halvt varv.

Snygg figur!

Men du har tagit fel på vilka par som är varandras komplexkonjugat.

På rektangulär form är a+bi och a-bi varandras komplexkonjugat, men du har parat ihop a+bi med -a-bi.

Ett komplext tal $z$ och dess komlexkonjugat $\bar{z}$ har alltså de egenskaperna att $Re(z)=Re(\bar{z})$ och $Im(z)=-Im(\bar{z})$. 

Jag förstod att det blivit fel när jag började multiplicera ihop de "falska paren"...

Försöker igen.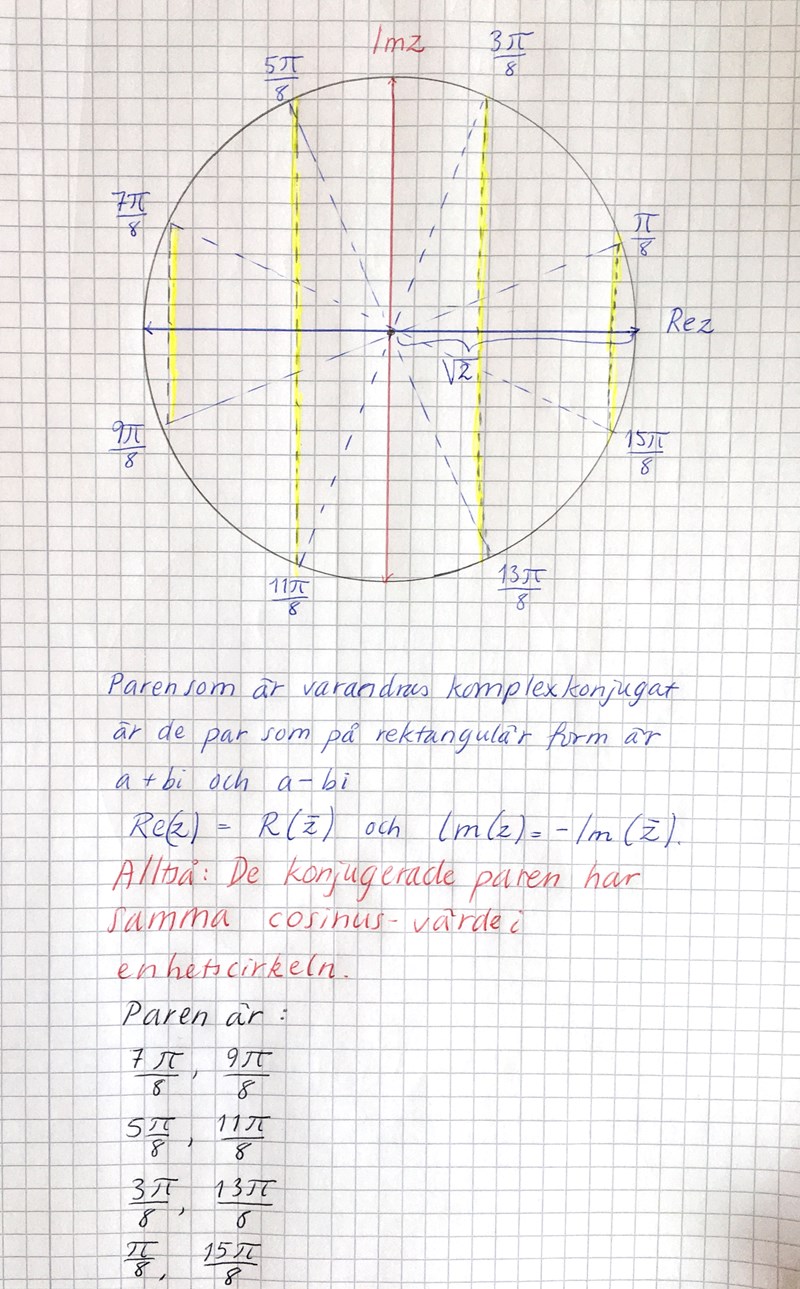

Kanelbullen skrev:

Jag förstod att det blivit fel när jag började multiplicera ihop de "falska paren"...

Försöker igen.

Snyggt!

Jag använder faktorsatsen, så att varje komplext tal ger upphov till en faktor som är lika med $x-\alpha$, där $\alpha$ är ett komplext tal.

Resultatet av dessa fyra multiplikationer bör bli de fyra reella faktorer som man söker efter i uppgiften.

$$\begin{gathered} (x-\sqrt{2}(\cos \left(\frac{7\mathrm{\pi }}{8}\right)+i\sin \left(\frac{7\mathrm{\pi }}{8}\right))·(x-\sqrt{2}\left(\cos \right(\frac{9\mathrm{\pi }}{8})+i\sin (\frac{9\mathrm{\pi }}{8}\left)\right) \left(I\right) \\ (x-\sqrt{2}(\cos \left(\frac{5\mathrm{\pi }}{8}\right)+i\sin \left(\frac{5\mathrm{\pi }}{8}\right))·(x-\sqrt{2}\left(\cos \right(\frac{11\mathrm{\pi }}{8})+i\sin (\frac{11\mathrm{\pi }}{8}\left)\right) \\ (x-\sqrt{2}(\cos \left(\frac{3\mathrm{\pi }}{8}\right)+i\sin \left(\frac{3\mathrm{\pi }}{8}\right))·(x-\sqrt{2}\left(\cos \right(\frac{13\mathrm{\pi }}{8})+i\sin (\frac{13\mathrm{\pi }}{8}\left)\right) \\ (x-\sqrt{2}(\cos \left(\frac{\mathrm{\pi }}{8}\right)+i\sin \left(\frac{\mathrm{\pi }}{8}\right))·(x-\sqrt{2}\left(\cos \right(\frac{15\mathrm{\pi }}{8})+i\sin (\frac{15\mathrm{\pi }}{8}\left)\right) \end{gathered}$$

Jag skulle behöva ytterligare lite hjälp eftersom jag inte känner mig så säker på polär form.

Om vi börjar med den första multiplikationen (I) så får jag det till

$x^2-\mathit{x}\mathbf{·}\sqrt{\mathbf{2}}\mathbf{\left(}\mathit{c}\mathit{o}\mathit{s}\mathbf{\right(}\frac{\mathbf{9}\mathbf{\pi }}{\mathbf{8}}\mathbf{)}\mathbf{+}\mathit{i}\mathit{s}\mathit{i}\mathit{n}\mathbf{(}\frac{\mathbf{9}\mathbf{\pi }}{\mathbf{8}}\mathbf{\left)}\mathbf{\right)}\mathbf{-}\mathit{x}\mathbf{·}\sqrt{\mathbf{2}}\mathbf{\left(}\mathit{c}\mathit{o}\mathit{s}\mathbf{\right(}\frac{\mathbf{7}\mathbf{\pi }}{\mathbf{8}}\mathbf{)}\mathbf{+}\mathit{i}\mathit{s}\mathit{i}\mathit{n}\mathbf{(}\frac{\mathbf{7}\mathbf{\pi }}{\mathbf{8}}\mathbf{\left)}\mathbf{\right)}\mathbf{ }+2$.

+2 får jag som sista term eftersom när jag multiplicerar de båda komplexa talen med varandra så multiplicerar jag absolutbeloppen och adderar argumenten vilket ger absolutbeloppet 2 och realdelen cos 2pi vilket är detsamma som 1, samt imaginärdelen sin 2pi vilket är detsamma som 0:

$2·1+0=2.$

Jag har alltså adderat vinklarna på följande sätt:

$\frac{9\mathrm{\pi }}{8}+\frac{7\mathrm{\pi }}{8}=\frac{16\mathrm{\pi }}{8}=\mathbf{2}\mathbf{\pi }.$

Jag behöver alltså vägledning vad gäller den mittersta termen. Jag skulle kunna bryta ut x. Sedan vet jag att $-\sqrt{2}-\sqrt{2} =2\sqrt{2}$. Men hur gör jag nu med vinklarna vid subtraktion? Jag ska behandla realdel och imaginärdel var för sig förstår jag, liksom man gör när man räknar med komplexa tal på rektangulär form. 

Den mittersta termen skulle kunna bli $-\left(2\sqrt{2}\right)(nånting med \cos och i\sin )x.$

Du får mycket enklare beräkningar om du väljer att skriva konjugatet till a+bi som a-bi istället för att ha olika vinklar. Välj alltså vinkeln $\frac{-7 \pi}{8}$ som konjugat till $frac{7 \pi}{8}$ istället för $frac{9 \pi}{8}$.

Tack Smaragdalena!

Jag har suttit länge nu och klurat på hur jag ska göra för att multiplicera de två första kojugerade paren av rötter. Nu har jag gjort så som du skrev och helt enkelt satt ett minustecken framför vinkeln för att få konjugatet. Eftersom två konjugerade komplexa tal ligger symmetriskt med avseende på den reella talaxeln i det komplexa talplanet, så är ju detta ett bra alternativ att uttrycka de två olika vinklarna. Ändå återstår för mig att lösa hur jag förenklar

$-x·\sqrt{2}\left(\cos \right(-\frac{7\mathrm{\pi }}{8})+i\sin (-\frac{7\mathrm{\pi }}{8})-x·\sqrt{2}(\cos \left(\frac{7\mathrm{\pi }}{8}\right)+i\sin \left(\frac{7\mathrm{\pi }}{8}\right).$

Jag ser att jag kan bryta ut x och jag vet att jag kan skriva $-\sqrt{2}-\sqrt{2}$ som $2\sqrt{2},$ men hur gör jag med vinklarna?

$(x-\sqrt{2}(\cos \left(\frac{7\mathrm{\pi }}{8}\right)+i\sin \left(\frac{7\mathrm{\pi }}{8}\right))·(x-\sqrt{2}\left(\cos \right(-\frac{7\mathrm{\pi }}{8})+i\sin (-\frac{7\mathrm{\pi }}{8}\left)\right) = {\mathit{x}}^{\mathbf{2}\mathbf{ }}\mathbf{-}\mathbf{2}\sqrt{\mathbf{2}}\mathbf{(}\mathbf{ }\mathbf{.}\mathbf{.}\mathbf{.}\mathbf{ }\mathbf{)}\mathit{x}\mathbf{+}\mathbf{2}$

En annan fundering jag har:

Kan man använda att $(a+ib)(a-ib)=a^2+b^2$?

Och vad blir i så fall $\left(\sqrt{2}\right(\cos \left(\frac{7\mathrm{\pi }}{8}\right)+i\sin {\left(\frac{7\mathrm{\pi }}{8}\right))}^2$?

Nu har jag även räknat om de komplexa talen till rektangulär form och då fick jag ungefärliga värden på

$z = -1,31+0,54i$  och konjugatet är då $-1,31-0,54i$.

Då har vi att $-(-1,31+0,54i)-(-1,31-0.54i) = 2,62$.

Jag skulle då chansa på att vinkeln på polär form uttryckt i radianer ska vara $\frac{\mathrm{\pi }}{8}$ eftersom $2\sqrt{2}\cos \left(\frac{\mathrm{\pi }}{8}\right)\approx 2,61$vilket ligger väldigt nära 2,62.

Så nu har jag kommit fram till den första av de fyra faktorerna och den är

$x^2-2\sqrt{2}\cos \left(\frac{\mathrm{\pi }}{8}\right)x+2.$

Men hur ska jag göra om jag inte vill gå denna omväg?

Utnyttja att cos(-v)=cos(v) och att sin(-v)=-sin(v).

Skriv om från (x-(a+bi))(x-(a-bi)) till ((x-a)-b)((x-a)+b) och använd konjugatregeln.

Visa hur långt du ahr kommit med hjälp av de här tipsen om du behöver mer hjälp.