Faktorsatsen
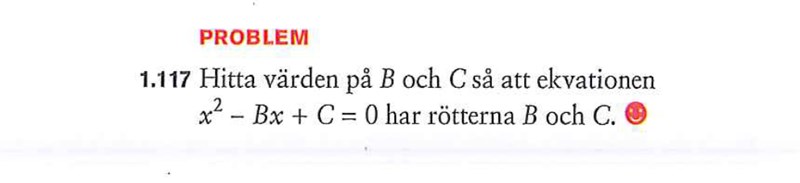
Okej , jag förstår inte hur man löser detta men enda jag vet är att
om lösningen ska vara B och C kan man skriva det som
(x-B) (x-C)
men hur ska man vidare sen?
mvh
Bra början!
Jag hoppas att du menar att polynomet i vänsterledet kan skrivas . I så fall stämmer det.
Du kan nu gå tillväga på två olika sätt. Pröva gärna båda!
- Det måste gälla att . Multiplicera ihop högerledets faktorer och jämför de båda sidorna. För att uttrycken ska vara identiska för alla möjliga värden på måste det gälla att koefficienterna framför -termerna och -termerna ska vara lika och att konstanttermerna ska vara lika. Det ger dig två ekvationer för och .
- Lös ut ur ekvationen genom kvadratkomplettering eller med pq-formeln. De två lösningarna och ska då vara lika med respektive .
Visa gärna dina försök.
Yngve skrev:Bra början!
Jag hoppas att du menar att polynomet i vänsterledet kan skrivas . I så fall stämmer det.
Du kan nu gå tillväga på två olika sätt. Pröva gärna båda!
- Det måste gälla att . Multiplicera ihop högerledets faktorer och jämför de båda sidorna. För att uttrycken ska vara identiska för alla möjliga värden på måste det gälla att koefficienterna framför -termerna och -termerna ska vara lika och att konstanttermerna ska vara lika. Det ger dig två ekvationer för och .
- Lös ut ur ekvationen genom kvadratkomplettering eller med pq-formeln. De två lösningarna och ska då vara lika med respektive .
Visa gärna dina försök.
Jag kommer tyvärr vidare ändå ... 
Du har kommit fram till att x2-Bx+C = x2-Cx-Bx+BC (jag har ite kontrollräknat). Om detta skall stämma så måste koefficienterna för x2-termen och för x-termen vara samma, och konstanttermen måste vara samma. Detta betyder att -B=-B-C och att C=BC. Du har alltså ett ekvationssystem med 2 ekvationer och 2 variabler. Kommer du ihåg från Ma2 hur man löser det?
Smaragdalena skrev:Du har kommit fram till att x2-Bx+C = x2-Cx-Bx+BC (jag har ite kontrollräknat). Om detta skall stämma så måste koefficienterna för x2-termen och för x-termen vara samma, och konstanttermen måste vara samma. Detta betyder att -B=-B-C och att C=BC. Du har alltså ett ekvationssystem med 2 ekvationer och 2 variabler. Kommer du ihåg från Ma2 hur man löser det
jag kan nog lösa ekvationssytemet men varför ska koefficienter och konstanter ska vara lika, kan du förklara förstår inte det
Du kan ta fallet med två förstagradspolynom istället, det är enklare.
Tänk dig två polynom och .
Dessa kan representeras av två linjer i ett koordinatsystem (enligt ).
För att dessa linjer ska vara identiska (dvs sammanfalla för alla möjliga värden på ) så måste och . Är du med på det?
Det innebär att för att våra polynom och ska vara identiska (dvs ha samma värde för alla möjliga värden på ) så måste och . Är du med på det?
=====
Exakt samma sak gäller för andragradspolynom
Tänk dig två polynom och .
Dessa kan representeras av två parabler i ett koordinatsystem.
För att dessa parabler ska vara identiska (dvs sammanfalla för alla möjliga värden på ) så måste , och . Är du med på det?
Det innebär att för att våra polynom och ska vara identiska (dvs ha samma värde för alla möjliga värden på ) så måste , och . Är du med på det?
och är koefficienterna framför -termerna.
och är koefficienterna framför -termerna.
och är konstanttermerna.
Blev det klarare då?
Klicka här för utökning/generalisering
Samma sak gäller för alla polynom, oavsett gradtal: För att två polynom ska vara identiska måste alla korresponderande koefficienter vara lika stora.
Yngve skrev:Du kan ta fallet med två förstagradspolynom istället, det är enklare.
Tänk dig två polynom och .
Dessa kan representeras av två linjer i ett koordinatsystem (enligt ).
För att dessa linjer ska vara identiska (dvs sammanfalla för alla möjliga värden på ) så måste och . Är du med på det?
Det innebär att för att våra polynom och ska vara identiska (dvs ha samma värde för alla möjliga värden på ) så måste och . Är du med på det?
=====
Exakt samma sak gäller för andragradspolynom
Tänk dig två polynom och .
Dessa kan representeras av två parabler i ett koordinatsystem.
För att dessa parabler ska vara identiska (dvs sammanfalla för alla möjliga värden på ) så måste , och . Är du med på det?
Det innebär att för att våra polynom och ska vara identiska (dvs ha samma värde för alla möjliga värden på ) så måste , och . Är du med på det?
Det förstår jag absolut 😊
Swateie skrev:Yngve skrev: Är du med på det??
Det förstår jag absolut 😊
Så är B = 1
och
-B = -C-B
det kanske är fel 😑




