Fartkamera

Hej, jag ska lösa uppgiften ovan och jag började med att ta fram en formel och jag gjorde så här:
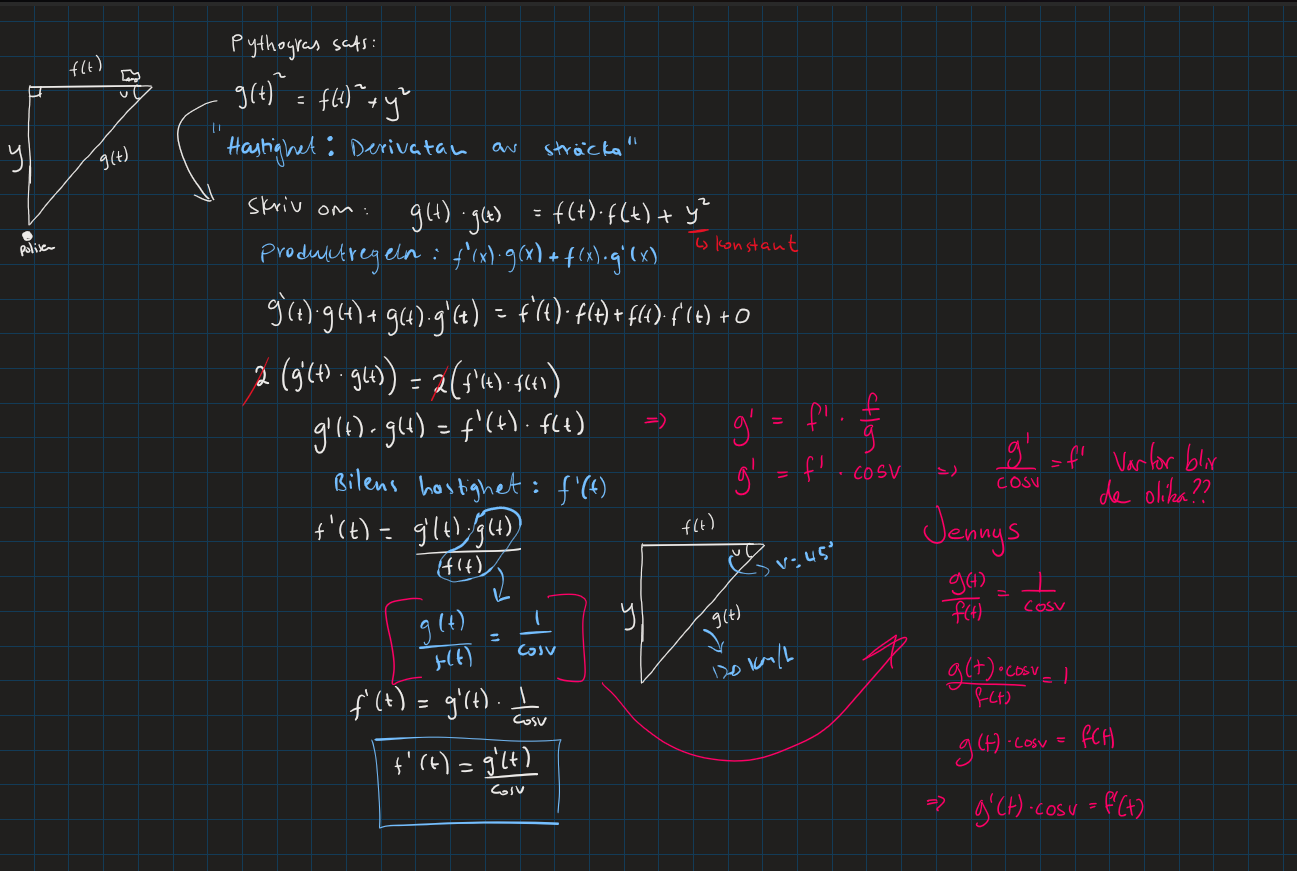
Men min lärare har skrivit i rött på sidan och har kommit fram till en annan formel. Hon säger att vi kan derivera så här för att cosv är konstant, men jag tycker att det beror på tiden och eftersom får vi olika vinklar beroende på hur långt bilen har färdats (eller tänker jag fel?).
Min lärarens uträkning.
I sambandet beror vänsterledet av tidsvariabeln, vilket innebär att högerledet också gör det. Du har helt rätt och man kan alltså inte anta att är konstant.
Om man använder sig av kedjeregeln, så kan man hitta sambandet mellan och utan att göra något explicit antagande om att (inte) är konstant:
Pythagoras sats ger , där är konstant.
Kedjeregeln ger att .
VL kan under patologiska förhållande vara konstant vilket skulle kunna motivera att cos v = konst, men inte i denna uppgift. Man ser det kanske tydligare via
tan v = y/f(t)
där y>0 är en konstant och f>0 en icke-konstant funktion (i så fall står bilen still).

