Fasskillnad i parallellkopplad krets med kondensator (AC)
Hej, håller på med med växelström och tycker det är rätt svårt. Är fast på uppgift 8.8a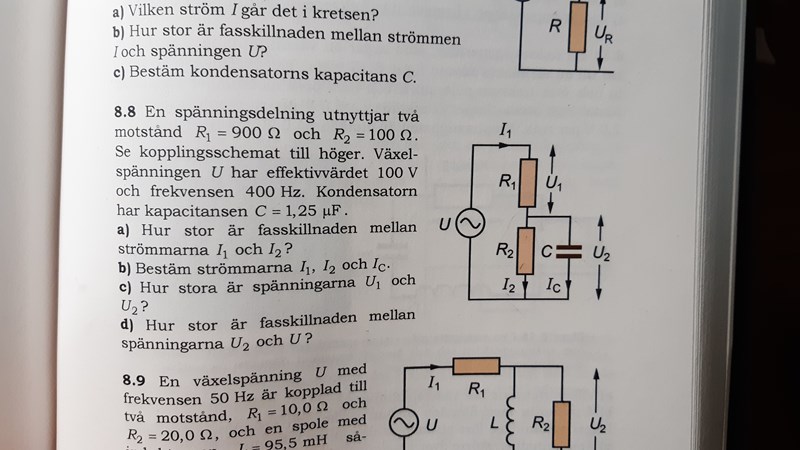 Jag har beräknat att impedansen är 318 Ohm i kondensatorn och jag antar att jag ska göra ett visardiagram för R2 och kondensatorn men vet inte vad som ska va på axlarna. Jag kan väl inte sätta resistansen på axlarna? Får en vinkel på ungefär 74 grader när jag gör det vilket är fel. Någon som vet hur jag ska göra
Jag har beräknat att impedansen är 318 Ohm i kondensatorn och jag antar att jag ska göra ett visardiagram för R2 och kondensatorn men vet inte vad som ska va på axlarna. Jag kan väl inte sätta resistansen på axlarna? Får en vinkel på ungefär 74 grader när jag gör det vilket är fel. Någon som vet hur jag ska göra
Det du tagit fram är fasförskjutningen för strömmen genom , alltså ca. .
Det finns flera sätt att göra på men det enklaste bör vara att uttrycka:
Detta ger ca. . Vad säger facit?
Hej, tack för svar men pratade med läraren innan jag såg att du svarat och han sa att vi inte behöver kunna räkna på parallellkopplade kretsar när det är växelström. Men bara så att du vet så har du nog gjort något fel i din beräkning. Svaret är 17,4 °
qwerty1234 skrev:Hej, tack för svar men pratade med läraren innan jag såg att du svarat och han sa att vi inte behöver kunna räkna på parallellkopplade kretsar när det är växelström. Men bara så att du vet så har du nog gjort något fel i din beräkning. Svaret är 17,4 °
Japp. Jag räknade av någon anledning ut fasskillnaden mellan och istället. För din info, eftersom fasskillnaden mellan och är så får vi:
Nu behöver jag ju som sagt inte kunna det men vad är J i din uträkning? Är det en konstant eller en variabel jag jag beräkna värdet på?
qwerty1234 skrev:
Nu behöver jag ju som sagt inte kunna det men vad är J i din uträkning? Är det en konstant eller en variabel jag jag beräkna värdet på?
Det är den imaginära enheten . Du har att impedansen för en kondensator är:
I ditt fall har du:
Eftersom du har att får du:
Du kan annars skriva den med ingenjörsnotation som:
Ahh okej, fattar nu. Tack för hjälpen!


