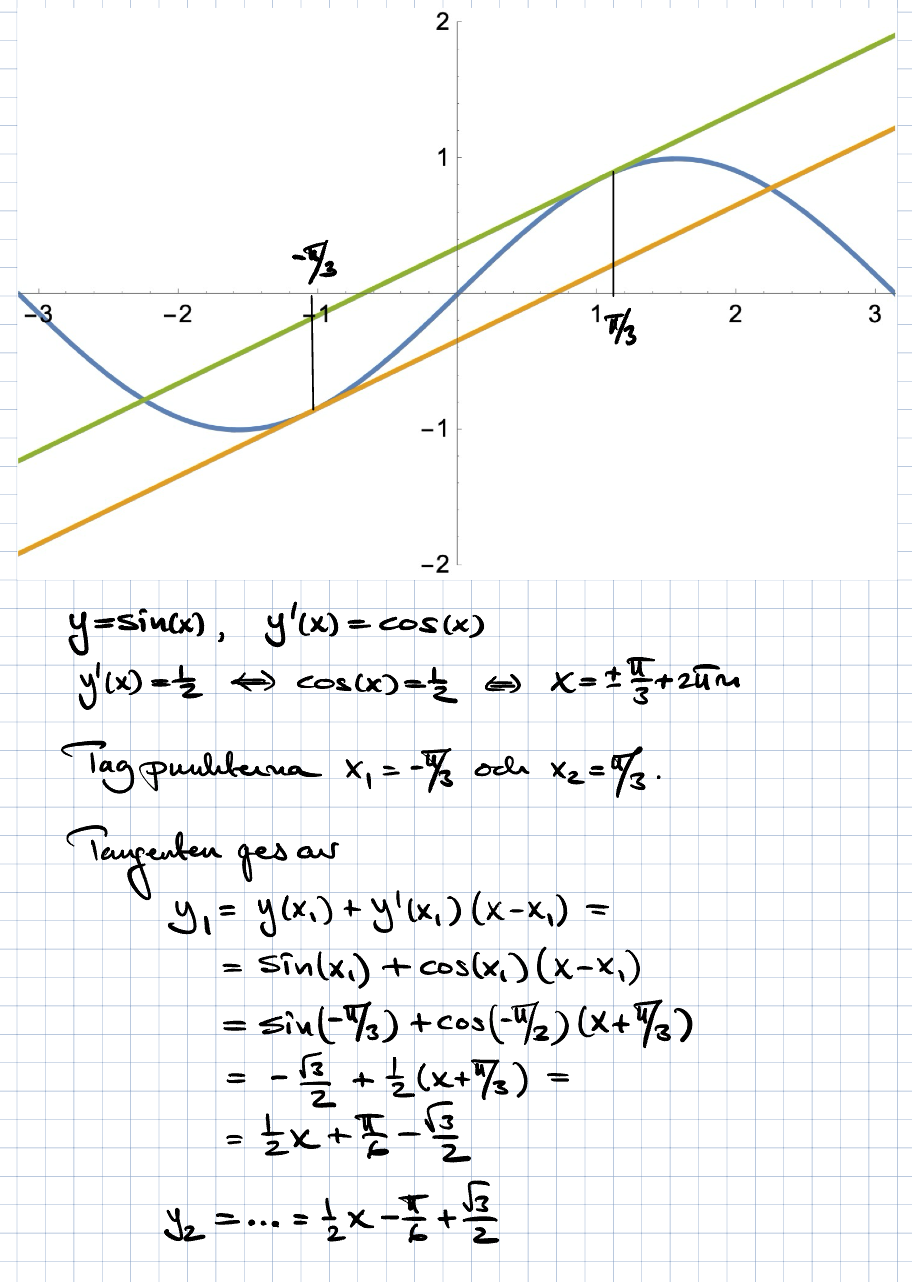
Fastnat - Ekvationen för 2 tangenter
Hej! Jag har fastnat halvvägs genom lösningen till denna uppgift: Bestäm exakt ekvationen för två tangenter till y = sin x som har lutningen 0,5.
Jag vet att cos x = 0,5 och att x = + n * .
Vad är nästa steg? Tacksam för hjälp.
Vi har att tangentens ekvation är kx+m=y och k=0.5 samt att tangenterna skär sin(x) då x=+-pi/3 så testa att använda denna information för att hitta ekvationerna.
Jag försökte prova med y = 0,5*pi/3 + m men nu har vi 2 okända. Ersätter jag y med sinpi/3
får jag m till ungefär 1,65 (om jag räknar med positiva pi/3). Blir ena svaret i så fall y = 0,5x+1,65?
Det har jag svårt att tro eftersom facits lösning såg ut såhär men jag förstår inte den.

Dr.scofield skrev:Jag försökte prova med y = 0,5*pi/3 + m men nu har vi 2 okända. Ersätter jag y med sinpi/3
får jag m till ungefär 1,65 (om jag räknar med positiva pi/3). Blir ena svaret i så fall y = 0,5x+1,65?
Det har jag svårt att tro eftersom facits lösning såg ut såhär men jag förstår inte den.
Är du säker på att du ränkade rätt?
Sin(pi/3)=sqrt(3)/2 -》sqrt(3)/2=0.5×pi/3+m -》sqrt(3)/2-pi/6=m -》y=0.5x+sqrt(3)/2-pi/6
Hur vet jag från början att sin(pi/3) har sqrt(3)/2 som exakta värde? Uppgiften skulle lösas utan miniräknare.
Jag tror att det står på formelbladet för matte 4, kan ha fel.
Det stämmer! Glömde bort det helt. Nu fick jag dessutom rätt svar. Tack!
Jag fick svaret y1 = 0,5x+sqrt(3)/2-0,5pi/3 och inte 0,5pi/6. Hur får jag 6an?