Favoritegenskaper hos primtal?
Hej!
Jag läser en kurs i elementär talteori, där det nämns att primtal har vissa speciella egenskaper som kan upplevas som intressanta eller vackra. Jag ville därför fråga er om ni har någon speciell aspekt av primtal som ni personligen är förtjusta i?
Jag personligen uppskattar beskrivningen av primtal som siffrornas grundämnen, och tycker det är intressant att de är oändligt många (hur kan ett primtal med en miljon siffror inte vara delbart med NÅGOT annat än 1 och sig självt!?), och att även om de tycks bli mer och mer utspridda ju längre ut man kommer på tallinjen, så tycks de ändå inte bli utspridda med oändligt stora mellanrum sinsemellan. Tycker även att det allra första "mellanrumsbeviset" av Zhang, där han visade att det åtminstone finns oändligt många primtal som skiljer sig åt med högst 70 miljoner, är lite charmigt då det på något sätt illustrerar hur matematiska/talteoretiska resultat kan vara så intressanta och samtidigt ointressanta på en och samma gång, på något sätt :)
Snarare analytisk talteori, men jag tycker det är otroligt fascinerande att man kan studera hur primtalen är distribuerade med hjälp av analytiska metoder och studier kring Riemanns zetafunktion. Särskilt eftersom relevanta samband mellan dem sker i de komplexa talen.
Faktumet att komplexa tal, speciella funktioner, deras rötter och primtal är relaterade är så otroligt coolt!
En annan sak är att man kan hitta ett segment på tallinjen utan primtal som är hur lång som helst. (alltså finns det ett segment på tallinjen där det inte existerar några primtal på tal, tal, tal, osv. Detta är inte heller särskilt svårt att bevisa:
Om man kollar på (för stora ) kommer vara delbart med 2 eftersom är jämnt, kommer vara delbart med 3 eftersom är en multipel av 3, osv hela vägen upp till att är delbart med .
Alla tal mellan till delbart något tal och därmed inte ett primtal.
Samtidigt finns det oändligt många!
(Egentligen kanske detta inte är en särskilt märkvärdig egenskap eftersom samma egenskap existerar exempelvis hos kvadraterna, men ändå!)
AlexMu skrev:Snarare analytisk talteori, men jag tycker det är otroligt fascinerande att man kan studera hur primtalen är distribuerade med hjälp av analytiska metoder och studier kring Riemanns zetafunktion. Särskilt eftersom relevanta samband mellan dem sker i de komplexa talen.
Faktumet att komplexa tal, speciella funktioner, deras rötter och primtal är relaterade är så otroligt coolt!
En annan sak är att man kan hitta ett segment på tallinjen utan primtal som är hur lång som helst. (alltså finns det ett segment på tallinjen där det inte existerar några primtal på tal, tal, tal, osv. Detta är inte heller särskilt svårt att bevisa:
Om man kollar på (för stora ) kommer vara delbart med 2 eftersom är jämnt, kommer vara delbart med 3 eftersom är en multipel av 3, osv hela vägen upp till att är delbart med .
Alla tal mellan till delbart något tal och därmed inte ett primtal.
Samtidigt finns det oändligt många!
(Egentligen kanske detta inte är en särskilt märkvärdig egenskap eftersom samma egenskap existerar exempelvis hos kvadraterna, men ändå!)
Intressant, tack för ditt svar! :D
Jag tycker att det är jätteintressant det där med att man kan hitta primtalsfria segment som är hur långa som helst. Kan dom vara oändligt långa också? Det känns som att svaret blir "nej" om man försöker få ihop det med att det också finns oändligt många primtal med en finit maxdifferens...?
Intressant också att relevanta samband mellan primtal sker i dom komplexa talen. Riemanns zetafunktions implikation för primtalsdistributionen är något som jag inte förstår ännu - såg en video där du Sautoy beskrev det tyyp som att implikationen i så fall är att primtalen är jämnt distributerade men utan något tydligt inneboende mönster, typ att man inte kan säga exakt var nästa primtal kommer att vara (som det kanske märks så vet jag knappt själv vad jag pratar om nu!)
Jag tror det finns nån sats som säger ungefär att det alltid finns ett primtal mellan n och 2n.
ytrewq skrev:Jag personligen uppskattar beskrivningen av primtal som siffrornas grundämnen, ...
På nordsamiska heter primtal 'álgolohku'.
Efterledet 'lohku' betyder rätt och slätt tal.
Förledet 'álgo' står för något ursprungligt. Andra exempel är 'álgobáliid' (adverb: i begynnelsen), 'álgoálbmot' (urfolk) och 'álgoávnnas' (råämne).
Däremot heter grundämne 'vuođđoávnnas', där 'vuođđu' betyder grund (som man bygger hus på). Lite trist, kanske.
Bara lite trivia, angående "siffrors grundämnen" som jag tyckte var en utmärkt benämning.
sictransit skrev:ytrewq skrev:Jag personligen uppskattar beskrivningen av primtal som siffrornas grundämnen, ...
På nordsamiska heter primtal 'álgolohku'.
Efterledet 'lohku' betyder rätt och slätt tal.
Förledet 'álgo' står för något ursprungligt. Andra exempel är 'álgobáliid' (adverb: i begynnelsen), 'álgoálbmot' (urfolk) och 'álgoávnnas' (råämne).
Däremot heter grundämne 'vuođđoávnnas', där 'vuođđu' betyder grund (som man bygger hus på). Lite trist, kanske.
Bara lite trivia, angående "siffrors grundämnen" som jag tyckte var en utmärkt benämning.
Vilket intressant tillägg, tack för det! :) Passade extra bra då jag nyligen blivit lite nyfiken på lingvistik! (efter att ha sett filmen Arrival)
Laguna skrev:Jag tror det finns nån sats som säger ungefär att det alltid finns ett primtal mellan n och 2n.
Ja. Jag tror denna sats heter ”Bertrands Postulate”.
ytrewq skrev:Intressant också att relevanta samband mellan primtal sker i dom komplexa talen. Riemanns zetafunktions implikation för primtalsdistributionen är något som jag inte förstår ännu - såg en video där du Sautoy beskrev det tyyp som att implikationen i så fall är att primtalen är jämnt distributerade men utan något tydligt inneboende mönster, typ att man inte kan säga exakt var nästa primtal kommer att vara (som det kanske märks så vet jag knappt själv vad jag pratar om nu!)
Jag tycker detta område är superintressant, så jag tänker babbla lite om det..
Man definierar primtalsfunktionen till att vara antalet primtal . Exempelvis är
eftersom det finns 4 primtal under 10: 2, 3, 5, 7.
.
Vidare definieras den logaritmiska integralen (för )
(på grund av den odefinierade punkten vid )
En mycket känd sats är primtalssatsen som säger att
Eller då att den relativa skillnaden mellan dessa två funktioner går mot 0 när . Det kanske också är intressant att detta är ekvivalent med att visa att riemanns zetafunktion inte har några rötter på linjen . På så sätt är riemannhypotesen ett mycket starkare påstående.
Då verkar det som att är en rätt bra approximation av , vilket stämmer enligt tabellen nedan (errorn är i procent):
Eftersom jag tycker detta är mycket intressant vill jag skriva en liten "heuristisk" härledning till varför i spoilern nedan.
Visa spoiler
Det jag kommer skriva här är baserat (i stort sett kopierat) från denna video. Mycket bra video och mycket tydligare än min kortfattade härledning här!
Igen, detta kommer vara mycket heuristiskt, så vi kan börja med att kika på hur bör förändras eller ""derivatan"" av . ökar med 1 varje gång är ett primtal.
Om vid någon punkt på tallinjen är exempelvis ungefär 1/5 av alla talen primtal kommer ju öka med 1 ungefär var femte tal, eller ungefär med varje tal, alltså densiteten av primtal vid denna punkt på tallinjen!
Då verkar förändringen av vara densiteten av primtalen, vi döper denna densitet till .
Iden är då att om vi kan hitta ungefär vad är så bör det vara "derivatan" av så kan vi sedan integrera det för att hitta ungefärliga värdet på . Vi gör detta genom att approximera på två olika sätt: Ett med primtal och ett utan primtal. Sedan, eftersom de approximerar samma sak bör de även approximera varandra.
Vi kan ju alltid primtalsfaktorisera ett heltal, så nu ska vi primtalsfaktorisera .
Vi låter och kikar på antalet 3:or som finns i faktoriseringen. Det finns tal som är delbara med som är . Det är . Därför är delbar med . Men vi har missat några!
Talet innehåller ju två treor eftersom det är , densamma gäller för . Vidare innehåller 3 st treor och just innehåller 4 st. Totalt finns det stycken treor i och beräknas på detta sätt:
och då för ett generellt primtal och talet gäller det att antalet faktorer av primtalet i ! är
Men alla termer efter den första är "små" och vi kan ignorera dem för vårt mål här. Vi ignorerar även avrundningen nedåt och då får vi att exponenten är ungefär . Detta gäller då för alla primtal och då får vi att
Där menar alla primtal mindre än eller lika med . Produkter är dock jobbiga och vi föredrar summor, vi kan "logaritmera" leden för att fixa detta (gör också approximationen lite bättre!)
Nu approximerar vi utan primtal!
Notera att
Men summan kan ses som en riemannsumma på och är alltså approximerad av integralen över :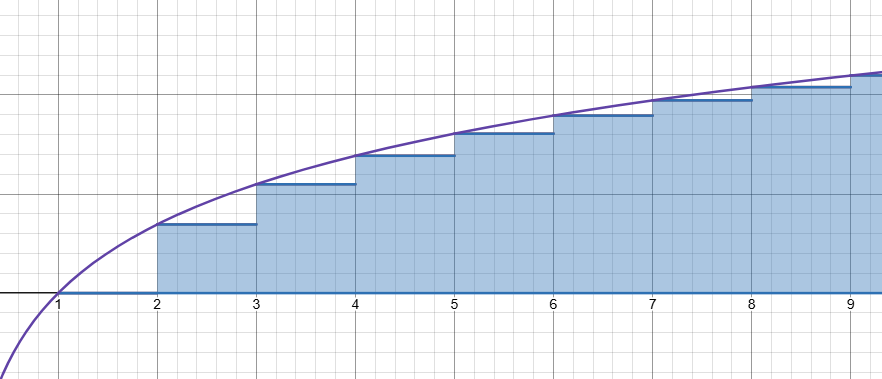 Alltså är
Alltså är
Denna integral kan vi beräkna, vilket ger oss att
Logaritmer är rätt små och vi har några konstanter, om vi kastar bort dem försämras inte approximationen särskilt mycket. Slutligen ger det oss att
Då har vi två stycken approximationer för och då bör de vara ungefär lika med varandra! Alltså:
Division med ger
Nu byter vi till eftersom vi ska prata om derivator.
Om vi vill ta derivatan av båda led här finns det inga problem med högerledet, men hur i hela friden kan vi ta derivatan av vänsterledet? Derivator är ju förändring, så vi kollar på hur VL förändras när ökar. Skillnaden mellan och (heltal) antingen är eller om är primtal.
Därför kan vi tänka oss att vi behöver ta något medelvärde för att få fram den ungefärliga förändringen och därmed "derivatan". Men "oddsen" att man adderar eller 0 är inte jämnt fördelad, det är ju om är primtal. Hur ofta sker det? Det var ju exakt definitionen av från tidigare!
Därför bör den ungefärliga förändringen på VL vara . Då bör detta vara "derivatan" av VL, i mycket stora citattecken.
Om vi då tar "derivatan" av båda led får vi
Vilket medför att
Om vi då integrerar densitetsfunktionen får vi alltså:
Så
Det finns en mycket fascinerande exakt formel för en kusin till . Vi kallar den för och den ökar med 1 vid ett primtal (som ) men även 1/2 vid en primtalskvadrat (tal på formen ), 1/3 vid en primtalskub, osv. Då gäller det för
Där innebär summan över alla där är de icke-triviala rötterna till riemanns zetafunktion. Detta kommer ursprungligen direkt från Riemann. Jag läste ett bevis av detta i denna bok. Jag tycker detta är så coolt eftersom det ska verkligen vara en likhet, inte en approximation. Det finns även ett (ganska enkelt) förhållande mellan och .
Tillägg: 10 jul 2025 12:18
Tror det ska vara i formeln för . Råkade nog skriva fel.
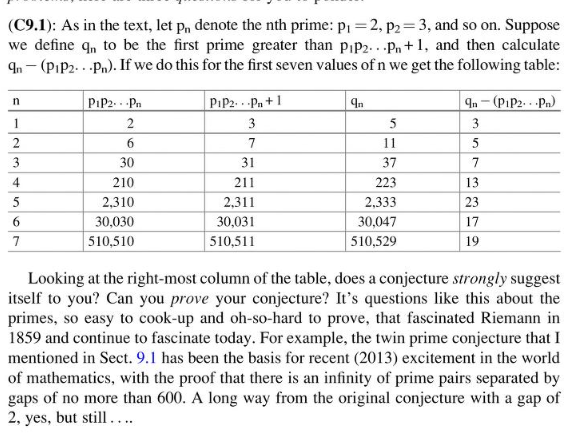
Något jag tycker är fascinerande är Goldbach's conjecture, eller rättare sagt tycker jag att det är fascinerande att man inte lyckats bevisa något som är rätt så uppenbart, trots all framgång man gjort inom matematiken.
Intressant video som jag såg för inte så länge sedan.
teknikomatte skrev:Något jag tycker är fascinerande är Goldbach's conjecture, eller rättare sagt tycker jag att det är fascinerande att man inte lyckats bevisa något som är rätt så uppenbart, trots all framgång man gjort inom matematiken.
Intressant video som jag såg för inte så länge sedan.
Det finns massvis med sådana här som är lätta att hitta på och tro stämmer, men myycket svåra att visa. Två exempel från en bok jag älskar (Inside Interesting Integrals):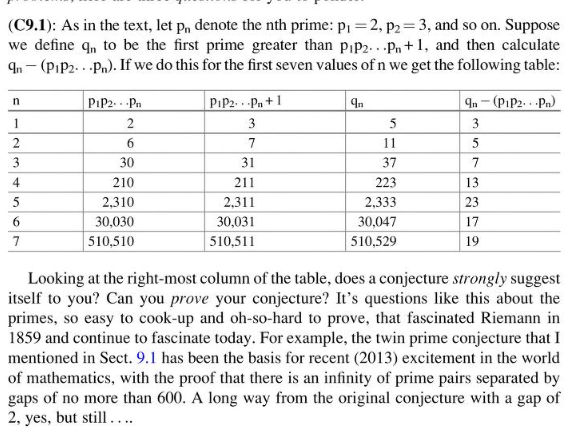

AlexMu skrev:teknikomatte skrev:Något jag tycker är fascinerande är Goldbach's conjecture, eller rättare sagt tycker jag att det är fascinerande att man inte lyckats bevisa något som är rätt så uppenbart, trots all framgång man gjort inom matematiken.
Intressant video som jag såg för inte så länge sedan.
Det finns massvis med sådana här som är lätta att hitta på och tro stämmer, men myycket svåra att visa. Två exempel från en bok jag älskar (Inside Interesting Integrals):
Nu är jag inte så insatt i talteori, men hur kommer det sig att de är så svåra att bevisa? Gissningsvis eftersom primtal inte följer någon direkt struktur och är oregelbundna i vart de befinner sig på tallinjen, men detta borde man väl kunna arbeta sig kring, då Euklides ändå lyckats bevisa att det finns oändligt med primtal t.ex, eller andra bevis gällande primtal?
Som sagt, inte så insatt men upplys mig gärna!
teknikomatte skrev:AlexMu skrev:...
Nu är jag inte så insatt i talteori, men hur kommer det sig att de är så svåra att bevisa? Gissningsvis eftersom primtal inte följer någon direkt struktur och är oregelbundna i vart de befinner sig på tallinjen, men detta borde man väl kunna arbeta sig kring, då Euklides ändå lyckats bevisa att det finns oändligt med primtal t.ex, eller andra bevis gällande primtal?
Som sagt, inte så insatt men upplys mig gärna!
Intressant fråga! Jag vet inte riktigt heller varför det är svårt att bevisa. Men jag tror snarare det har med att göra att många av dessa kända satser/hypoteser inom talteori är lätta att förstå. Det gör det mer bisarrt att det skulle vara så svårt att bevisa. Tre exempel är
Goldbach's conjecture, som du redan nämnt,
Twin Prime Conjecture, som säger att det finns oändligt många primtalstvillingar (primtal där differensen mellan dem är 2, exempelvis 5 och 7)
Fermats stora sats, som säger att ekvationen
där är positiva heltal och inte har några lösningar. Detta är bevisat men Fermat introducerade denna hypotes på 1600-talet och den bevisades 1994, alltså tog det över 300 år.
Dessa påståenden är ofta en rad långa, man behöver inte särskilt mycket bakgrund för att förstå dem, samtidigt är de mycket svåra att bevisa. Jag tror detta är vad som gör det överraskande.
Kan väl också slänga in Collatz Conjecture här, inte riktigt talteori, men fortfarande ett ganska enkelt påstående som inte är bevisat.
Ett annat exempel på en uppenbar* sats är the Jordan Curve Theorem, som säger (förenklat) att en kurva som är stängd (den "börjar" och "slutar" på samma ställe) och som skär sig själv delar upp planet i två delar, en insida och en utsida. Denna meme bild får denna sats att se otroligt trivial och uppenbar ut:

Tydligen är denna sats ganska svår att bevisa. *Dessa exempel på Jordan curves i bilden är egentligen missvisande och det är inte så uppenbart som man kanske kan tro, vilket tas upp här.
AlexMu skrev:teknikomatte skrev:AlexMu skrev:...
Nu är jag inte så insatt i talteori, men hur kommer det sig att de är så svåra att bevisa? Gissningsvis eftersom primtal inte följer någon direkt struktur och är oregelbundna i vart de befinner sig på tallinjen, men detta borde man väl kunna arbeta sig kring, då Euklides ändå lyckats bevisa att det finns oändligt med primtal t.ex, eller andra bevis gällande primtal?
Som sagt, inte så insatt men upplys mig gärna!
Intressant fråga! Jag vet inte riktigt heller varför det är svårt att bevisa. Men jag tror snarare det har med att göra att många av dessa kända satser/hypoteser inom talteori är lätta att förstå. Det gör det mer bisarrt att det skulle vara så svårt att bevisa. Tre exempel är
Goldbach's conjecture, som du redan nämnt,
Twin Prime Conjecture, som säger att det finns oändligt många primtalstvillingar (primtal där differensen mellan dem är 2, exempelvis 5 och 7)
Fermats stora sats, som säger att ekvationen
där är positiva heltal och inte har några lösningar. Detta är bevisat men Fermat introducerade denna hypotes på 1600-talet och den bevisades 1994, alltså tog det över 300 år.
Dessa påståenden är ofta en rad långa, man behöver inte särskilt mycket bakgrund för att förstå dem, samtidigt är de mycket svåra att bevisa. Jag tror detta är vad som gör det överraskande.Kan väl också slänga in Collatz Conjecture här, inte riktigt talteori, men fortfarande ett ganska enkelt påstående som inte är bevisat.
Ett annat exempel på en uppenbar* sats är the Jordan Curve Theorem, som säger (förenklat) att en kurva som är stängd (den "börjar" och "slutar" på samma ställe) och som skär sig själv delar upp planet i två delar, en insida och en utsida. Denna meme bild får denna sats att se otroligt trivial och uppenbar ut:
Tydligen är denna sats ganska svår att bevisa. *Dessa exempel på Jordan curves i bilden är egentligen missvisande och det är inte så uppenbart som man kanske kan tro, vilket tas upp här.
Väldigt intressant! Nästan så att man vill läsa någon kurs eller fördjupa sig mer inom detta.
Hade varit coolt att se någon lyckas lösa något av problemen under ens egen livstid :P
teknikomatte skrev:AlexMu skrev:...
Väldigt intressant! Nästan så att man vill läsa någon kurs eller fördjupa sig mer inom detta.
Hade varit coolt att se någon lyckas lösa något av problemen under ens egen livstid :P
Ja absolut! Vi får se!
En av de obevisade problemen inom analytisk talteori som jag tycker är mycket intressant är just riemannhypotesen, ett mycket välkänt problem från 1850-talet.
Vi är inte de enda som hoppas att vi ser dessa problem lösas under vår livstid. Jag tycker dessa utdrag från boken Gamma: Exploring Eulers Constant är roliga gällande det: 
 Jag minns också att någon matematiker (gissar på Hilbert?) sa att om de kunde bli uppväckta typ 100+ år i framtiden skulle deras första fråga vara om denna hypotes hade bevisats. Dock kan jag inte hitta det citatet i någon av mina böcker om talteori.
Jag minns också att någon matematiker (gissar på Hilbert?) sa att om de kunde bli uppväckta typ 100+ år i framtiden skulle deras första fråga vara om denna hypotes hade bevisats. Dock kan jag inte hitta det citatet i någon av mina böcker om talteori.
AlexMu skrev:ytrewq skrev:Intressant också att relevanta samband mellan primtal sker i dom komplexa talen. Riemanns zetafunktions implikation för primtalsdistributionen är något som jag inte förstår ännu - såg en video där du Sautoy beskrev det tyyp som att implikationen i så fall är att primtalen är jämnt distributerade men utan något tydligt inneboende mönster, typ att man inte kan säga exakt var nästa primtal kommer att vara (som det kanske märks så vet jag knappt själv vad jag pratar om nu!)
Jag tycker detta område är superintressant, så jag tänker babbla lite om det..
Man definierar primtalsfunktionen till att vara antalet primtal . Exempelvis är
eftersom det finns 4 primtal under 10: 2, 3, 5, 7.
.
Vidare definieras den logaritmiska integralen (för )
(på grund av den odefinierade punkten vid )
En mycket känd sats är primtalssatsen som säger att
Eller då att den relativa skillnaden mellan dessa två funktioner går mot 0 när . Det kanske också är intressant att detta är ekvivalent med att visa att riemanns zetafunktion inte har några rötter på linjen . På så sätt är riemannhypotesen ett mycket starkare påstående.
Då verkar det som att är en rätt bra approximation av , vilket stämmer enligt tabellen nedan (errorn är i procent):
Eftersom jag tycker detta är mycket intressant vill jag skriva en liten "heuristisk" härledning till varför i spoilern nedan.Visa spoiler
Det jag kommer skriva här är baserat (i stort sett kopierat) från denna video. Mycket bra video och mycket tydligare än min kortfattade härledning här!
Igen, detta kommer vara mycket heuristiskt, så vi kan börja med att kika på hur bör förändras eller ""derivatan"" av . ökar med 1 varje gång är ett primtal.
Om vid någon punkt på tallinjen är exempelvis ungefär 1/5 av alla talen primtal kommer ju öka med 1 ungefär var femte tal, eller ungefär med varje tal, alltså densiteten av primtal vid denna punkt på tallinjen!
Då verkar förändringen av vara densiteten av primtalen, vi döper denna densitet till .
Iden är då att om vi kan hitta ungefär vad är så bör det vara "derivatan" av så kan vi sedan integrera det för att hitta ungefärliga värdet på . Vi gör detta genom att approximera på två olika sätt: Ett med primtal och ett utan primtal. Sedan, eftersom de approximerar samma sak bör de även approximera varandra.
Vi kan ju alltid primtalsfaktorisera ett heltal, så nu ska vi primtalsfaktorisera .
Vi låter och kikar på antalet 3:or som finns i faktoriseringen. Det finns tal som är delbara med som är . Det är . Därför är delbar med . Men vi har missat några!
Talet innehåller ju två treor eftersom det är , densamma gäller för . Vidare innehåller 3 st treor och just innehåller 4 st. Totalt finns det stycken treor i och beräknas på detta sätt:
och då för ett generellt primtal och talet gäller det att antalet faktorer av primtalet i ! är
Men alla termer efter den första är "små" och vi kan ignorera dem för vårt mål här. Vi ignorerar även avrundningen nedåt och då får vi att exponenten är ungefär . Detta gäller då för alla primtal och då får vi attDär menar alla primtal mindre än eller lika med . Produkter är dock jobbiga och vi föredrar summor, vi kan "logaritmera" leden för att fixa detta (gör också approximationen lite bättre!)
Nu approximerar vi utan primtal!
Notera att
Men summan kan ses som en riemannsumma på och är alltså approximerad av integralen över :Alltså är
Denna integral kan vi beräkna, vilket ger oss att
Logaritmer är rätt små och vi har några konstanter, om vi kastar bort dem försämras inte approximationen särskilt mycket. Slutligen ger det oss att
Då har vi två stycken approximationer för och då bör de vara ungefär lika med varandra! Alltså:
Division med ger
Nu byter vi till eftersom vi ska prata om derivator.
Om vi vill ta derivatan av båda led här finns det inga problem med högerledet, men hur i hela friden kan vi ta derivatan av vänsterledet? Derivator är ju förändring, så vi kollar på hur VL förändras när ökar. Skillnaden mellan och (heltal) antingen är eller om är primtal.
Därför kan vi tänka oss att vi behöver ta något medelvärde för att få fram den ungefärliga förändringen och därmed "derivatan". Men "oddsen" att man adderar eller 0 är inte jämnt fördelad, det är ju om är primtal. Hur ofta sker det? Det var ju exakt definitionen av från tidigare!
Därför bör den ungefärliga förändringen på VL vara . Då bör detta vara "derivatan" av VL, i mycket stora citattecken.
Om vi då tar "derivatan" av båda led får vi
Vilket medför att
Om vi då integrerar densitetsfunktionen får vi alltså:
SåDet finns en mycket fascinerande exakt formel för en kusin till . Vi kallar den för och den ökar med 1 vid ett primtal (som ) men även 1/2 vid en primtalskvadrat (tal på formen ), 1/3 vid en primtalskub, osv. Då gäller det för
Där innebär summan över alla där är de icke-triviala rötterna till riemanns zetafunktion. Detta kommer ursprungligen direkt från Riemann. Jag läste ett bevis av detta i denna bok. Jag tycker detta är så coolt eftersom det ska verkligen vara en likhet, inte en approximation. Det finns även ett (ganska enkelt) förhållande mellan och .
Tillägg: 10 jul 2025 12:18
Tror det ska vara i formeln för . Råkade nog skriva fel.
Tack AlexMu för intressanta inlägg! Tyckte att primtalssatsen var intressant, betyder det att vid oändligheten så är pi(x) = li(x)? (rent teoretiskt). Jag ville även tolka det som att skillnaden mellan pi(x) och li(x) blir mindre och mindre ju högre x blir, men jag ser inget sådant undantagslöst mönster i tabellen över relativ error...!
Även spännande med jordans teorem för icke-intuitiva kurvor, och kul med lite roliga fakta om betydelsen av Riemann-hypotesen för matematikerna :D Jag gillar att lära mig om den aspekten av matematik också, alltså lite matematik-historia och anekdoter! Det finns då onekligen många excentriska typer i matematikens historia :)
Skillnaden relativt till storleken på funktionerna blir mindre, men det säger inte mycket om den exakta skillnaden mellan dem. Ett annat exempel är att den relativa errorn mellan och också är 0, även om de alltid är 1 ifrån varandra. Relativ error mellan och är också 0, fast den direkta differensen ökar!
I fallet med och kan du se att i tabellen så verkar vara större än . I varje värde jag inkluderade är det så. Alltså verkar det vara så att
men detta stämmer inte! Man vet inte vart detta sker för första gången, men differensen mellan funktionerna byter tecken oändligt många gånger! Det tycker jag verkligen tyder på att denna approximation är riktigt bra!
En annan mycket intressant hypotes som är relaterad till riemannhypotesen kallas för Mertens Conjecture.
Det finns en funktion som kallas för Möbius funktionen, som definieras enligt:
 (PA LaTeX låter mig inte göra fallindelning på detta sätt)
(PA LaTeX låter mig inte göra fallindelning på detta sätt)
Exempelvis är eftersom och då är . Hur som helst, från detta definieras mertens funktion enligt:
Mertens hypotes handlar om storleken på . Hypotesen var att för alla så är
Detta är relaterat till riemannhypotesen och är ett starkare påstående. Om detta skulle stämma skulle automatiskt även riemannhypotesen vara sann (Däremot skulle detta kunna vara falskt, men riemannhypotesen fortfarande sann).
Det är verifierat att olikheten stämmer för upp till , men det visade sig att denna hypotes inte är sann. Dock har man inget exakt motexempel än.
När jag hörde för första gången att man har verifierat riemannhypotesen upp till triljoner av rötter kändes det typ ”okej, vi har inget bevis men riemannhypotesen stämmer för så många rötter, den måste väl ändå vara sann?”. Men sedan har man detta problem, också med otroligt mycket numeriska beräkningar som tyder på att den är sann, fast det var den inte!
Sedan finns också detta utdrag från en bok (Prime Obsession, Derbyshire) som jag tycker är mycket intressant:
 jag har ingen som helst aning om vad denna funktion är och jag har inte lyckats hitta mycket om den. Är även bortrest och har inte tillgång till en dator! Den här boken använder en annan bok jag läser som källa, så den där -funktionen kanske dyker up där?
jag har ingen som helst aning om vad denna funktion är och jag har inte lyckats hitta mycket om den. Är även bortrest och har inte tillgång till en dator! Den här boken använder en annan bok jag läser som källa, så den där -funktionen kanske dyker up där?
Budskapet att det finns det som tyder på att hypotesen kan vara falsk är däremot spännande!
AlexMu skrev:Skillnaden relativt till storleken på funktionerna blir mindre, men det säger inte mycket om den exakta skillnaden mellan dem. Ett annat exempel är att den relativa errorn mellan och också är 0, även om de alltid är 1 ifrån varandra. Relativ error mellan och är också 0, fast den direkta differensen ökar!
I fallet med och kan du se att i tabellen så verkar vara större än . I varje värde jag inkluderade är det så. Alltså verkar det vara så att
men detta stämmer inte! Man vet inte vart detta sker för första gången, men differensen mellan funktionerna byter tecken oändligt många gånger! Det tycker jag verkligen tyder på att denna approximation är riktigt bra!
En annan mycket intressant hypotes som är relaterad till riemannhypotesen kallas för Mertens Conjecture.
Det finns en funktion som kallas för Möbius funktionen, som definieras enligt:
(PA LaTeX låter mig inte göra fallindelning på detta sätt)
Exempelvis är eftersom och då är . Hur som helst, från detta definieras mertens funktion enligt:
Mertens hypotes handlar om storleken på . Hypotesen var att för alla så är
Detta är relaterat till riemannhypotesen och är ett starkare påstående. Om detta skulle stämma skulle automatiskt även riemannhypotesen vara sann (Däremot skulle detta kunna vara falskt, men riemannhypotesen fortfarande sann).
Det är verifierat att olikheten stämmer för upp till , men det visade sig att denna hypotes inte är sann. Dock har man inget exakt motexempel än.
När jag hörde för första gången att man har verifierat riemannhypotesen upp till triljoner av rötter kändes det typ ”okej, vi har inget bevis men riemannhypotesen stämmer för så många rötter, den måste väl ändå vara sann?”. Men sedan har man detta problem, också med otroligt mycket numeriska beräkningar som tyder på att den är sann, fast det var den inte!
Sedan finns också detta utdrag från en bok (Prime Obsession, Derbyshire) som jag tycker är mycket intressant:
jag har ingen som helst aning om vad denna funktion är och jag har inte lyckats hitta mycket om den. Är även bortrest och har inte tillgång till en dator! Den här boken använder en annan bok jag läser som källa, så den där -funktionen kanske dyker up där?
Budskapet att det finns det som tyder på att hypotesen kan vara falsk är däremot spännande!
"Ett annat exempel är att den relativa errorn mellan x och x+1 också är 0, även om de alltid är 1 ifrån varandra." - är detta för att negativa x också inkluderas så att dom tar ut dom positiva? Tex -2 och -2+1 som jämnar ut 2 och 2+1?
I så fall förstår jag också varför det oändliga teckenbytet är bra!
Jättespännande med att Riemann-hypotesen kan visa sig vara falsk svindlande högt upp på "den kritiska linjen"! Nu backar jag diskussionen 2000 år, men det är egentligen fortfarande häftigt att tex Pythagoras sats är bevisat sann för varenda tänkbar rätvinklig triangel på en plan yta. Alltså, VARENDA en! Ett oändligt stort kliv fram jämfört med när människor tidigare sniffat på Pythagoras sats och gett ett fåtal konkreta exempel där den typen av samband håller.
Tack igen för ditt svar, det märks att du verkligen brinner för ämnet! Fint att se :)
Gällande relativ error är det snarare att den där ettan i skillnad mellan och är liten relativt till funktionsvärdena för stora . Om är en skillnad i 1 mellan funktionerna typ en miljondel av en procent av funktionsvärdena, nästan obetydligt.
För kanske (alla siffror här är påhittade) det finns något där och skiljer sig med typ 10000, men funktionsvärdena i sig ligger på ungefär . Då är 10000 hit och dit nästan ingenting. Relativt till storleken på funktionerna är errorn i princip obetydlig. Vi kan då säga att primtalssatsen garanterar att detta alltid stämmer.
Det skulle vara värsta chocken om hypotesen är falsk, jag vet inte riktigt vad jag själv tror egentligen! Och ja, det är fascinerande vad man kan bevisa! Att något stämmer för alla möjliga figurer, tal eller vad som helst.
Jag tyckte det var kul att se en tråd om primtal! Tack för att du skapade den. Själv tycker jag analytisk talteori är ett mycket mycket intressant, men också svårt ämne.
Jag köpte en bok förra året om zetafunktionen (Riemann’s Zeta Function, Edwards) och tog mig igen de första typ 2-3 kapitlen, men efter det märktes det verkligen att jag saknar kunskap för att faktiskt hänga med på allt som händer i boken! Så det har lett mig på andra vägar för att få en bättre grund inom analys. Kanske går bättre med boken snart!
ytrewq skrev:AlexMu skrev:Snarare analytisk talteori, men jag tycker det är otroligt fascinerande att man kan studera hur primtalen är distribuerade med hjälp av analytiska metoder och studier kring Riemanns zetafunktion. Särskilt eftersom relevanta samband mellan dem sker i de komplexa talen.
Faktumet att komplexa tal, speciella funktioner, deras rötter och primtal är relaterade är så otroligt coolt!
En annan sak är att man kan hitta ett segment på tallinjen utan primtal som är hur lång som helst. (alltså finns det ett segment på tallinjen där det inte existerar några primtal på tal, tal, tal, osv. Detta är inte heller särskilt svårt att bevisa:
Om man kollar på (för stora ) kommer vara delbart med 2 eftersom är jämnt, kommer vara delbart med 3 eftersom är en multipel av 3, osv hela vägen upp till att är delbart med .
Alla tal mellan till delbart något tal och därmed inte ett primtal.
Samtidigt finns det oändligt många!
(Egentligen kanske detta inte är en särskilt märkvärdig egenskap eftersom samma egenskap existerar exempelvis hos kvadraterna, men ändå!)Intressant, tack för ditt svar! :D
Jag tycker att det är jätteintressant det där med att man kan hitta primtalsfria segment som är hur långa som helst. Kan dom vara oändligt långa också? Det känns som att svaret blir "nej" om man försöker få ihop det med att det också finns oändligt många primtal med en finit maxdifferens...?
Intressant också att relevanta samband mellan primtal sker i dom komplexa talen. Riemanns zetafunktions implikation för primtalsdistributionen är något som jag inte förstår ännu - såg en video där du Sautoy beskrev det tyyp som att implikationen i så fall är att primtalen är jämnt distributerade men utan något tydligt inneboende mönster, typ att man inte kan säga exakt var nästa primtal kommer att vara (som det kanske märks så vet jag knappt själv vad jag pratar om nu!)
Ännu lite sjukare är att det finns godtyckligt långa följder där varje tal är delbart med k olika primtal, för varje k.
Det finns alltså exempelvis följder med en miljard på varandra följande tal där varje tal är delbart med minst en miljard olika primtal.
AlexMu skrev:Gällande relativ error är det snarare att den där ettan i skillnad mellan och är liten relativt till funktionsvärdena för stora . Om är en skillnad i 1 mellan funktionerna typ en miljondel av en procent av funktionsvärdena, nästan obetydligt.
För kanske (alla siffror här är påhittade) det finns något där och skiljer sig med typ 10000, men funktionsvärdena i sig ligger på ungefär . Då är 10000 hit och dit nästan ingenting. Relativt till storleken på funktionerna är errorn i princip obetydlig. Vi kan då säga att primtalssatsen garanterar att detta alltid stämmer.
Det skulle vara värsta chocken om hypotesen är falsk, jag vet inte riktigt vad jag själv tror egentligen! Och ja, det är fascinerande vad man kan bevisa! Att något stämmer för alla möjliga figurer, tal eller vad som helst.
Jag tyckte det var kul att se en tråd om primtal! Tack för att du skapade den. Själv tycker jag analytisk talteori är ett mycket mycket intressant, men också svårt ämne.
Jag köpte en bok förra året om zetafunktionen (Riemann’s Zeta Function, Edwards) och tog mig igen de första typ 2-3 kapitlen, men efter det märktes det verkligen att jag saknar kunskap för att faktiskt hänga med på allt som händer i boken! Så det har lett mig på andra vägar för att få en bättre grund inom analys. Kanske går bättre med boken snart!
Ah... Förstår! Tack, det var en tydlig förklaring! :)
Analytisk talteori vet jag vad det är, men kan ännu ingenting om det! Det känns intressant att man kan använda kontinuerlig matematik för att förstå diskret matematik... Finns något spännande i det! :)
Imponerande av dig att läsa matematiska böcker på fritiden, känns det som? Själv är jag inte på den nivån, men började nyligen läsa lite i Diaspora, där författaren har en examen i matematik och gärna tar in såna influenser i sina böcker! Gillar tanken på matematik-sci fi!
Smutsmunnen skrev:ytrewq skrev:AlexMu skrev:Snarare analytisk talteori, men jag tycker det är otroligt fascinerande att man kan studera hur primtalen är distribuerade med hjälp av analytiska metoder och studier kring Riemanns zetafunktion. Särskilt eftersom relevanta samband mellan dem sker i de komplexa talen.
Faktumet att komplexa tal, speciella funktioner, deras rötter och primtal är relaterade är så otroligt coolt!
En annan sak är att man kan hitta ett segment på tallinjen utan primtal som är hur lång som helst. (alltså finns det ett segment på tallinjen där det inte existerar några primtal på tal, tal, tal, osv. Detta är inte heller särskilt svårt att bevisa:
Om man kollar på (för stora ) kommer vara delbart med 2 eftersom är jämnt, kommer vara delbart med 3 eftersom är en multipel av 3, osv hela vägen upp till att är delbart med .
Alla tal mellan till delbart något tal och därmed inte ett primtal.
Samtidigt finns det oändligt många!
(Egentligen kanske detta inte är en särskilt märkvärdig egenskap eftersom samma egenskap existerar exempelvis hos kvadraterna, men ändå!)Intressant, tack för ditt svar! :D
Jag tycker att det är jätteintressant det där med att man kan hitta primtalsfria segment som är hur långa som helst. Kan dom vara oändligt långa också? Det känns som att svaret blir "nej" om man försöker få ihop det med att det också finns oändligt många primtal med en finit maxdifferens...?
Intressant också att relevanta samband mellan primtal sker i dom komplexa talen. Riemanns zetafunktions implikation för primtalsdistributionen är något som jag inte förstår ännu - såg en video där du Sautoy beskrev det tyyp som att implikationen i så fall är att primtalen är jämnt distributerade men utan något tydligt inneboende mönster, typ att man inte kan säga exakt var nästa primtal kommer att vara (som det kanske märks så vet jag knappt själv vad jag pratar om nu!)
Ännu lite sjukare är att det finns godtyckligt långa följder där varje tal är delbart med k olika primtal, för varje k.
Det finns alltså exempelvis följder med en miljard på varandra följande tal där varje tal är delbart med minst en miljard olika primtal.
Ja, alltså det är genuint jättekonstigt... Och intressant!
Har man hittat något konkret exempel ännu på en följd av sån slags följd av imponerande storlek? (längdmässigt eller stort k-mässigt)
Vad innebär det egentligen att det är sant för godtyckligt långa följder? Innebär det att man kan hitta en följd av i princip varje längd där detta gäller? Kan man rentav hitta en följd för bokstavligen varje längd?
Japp för bokstavligen varje längd.
De är naturligtvis ofantligt stora men man kan konstruera dem som lösningar till kongruenssystem.
Låt q_1 vara produkten av de första k primtalen.
q_2 vara produkten vara produkten till nästa k stycken primtal.
...
q_n vara produkten av primtal nummer (n-1)*k+1 till nk.
Kinesiska restsatsen säger då att följande kongruenssystem har en lösning:
x=1 mod q_1
x=2 mod q_2
...
x=n mod q_n
vilket innebär att x-n, x-n+1, x-n+2,...,x-1 alla har minst k olika primtalsdelare.
Satsen garanterar också att x är mindre än produkten av de kn första primtalen, så exempelvis: det finns en följd av en miljard på varandra följande tal, alla med minst en miljard olika primtalsdelare och talen i den följden är mindre än produkten av de 10^18 första primtalen (vilket natruligtvis är hysteriskt stort).
Smutsmunnen skrev:Japp för bokstavligen varje längd.
De är naturligtvis ofantligt stora men man kan konstruera dem som lösningar till kongruenssystem.
Låt q_1 vara produkten av de första k primtalen.
q_2 vara produkten vara produkten till nästa k stycken primtal.
...
q_n vara produkten av primtal nummer (n-1)*k+1 till nk.
Kinesiska restsatsen säger då att följande kongruenssystem har en lösning:
x=1 mod q_1
x=2 mod q_2
...
x=n mod q_n
vilket innebär att x-n, x-n+1, x-n+2,...,x-1 alla har minst k olika primtalsdelare.
Satsen garanterar också att x är mindre än produkten av de kn första primtalen, så exempelvis: det finns en följd av en miljard på varandra följande tal, alla med minst en miljard olika primtalsdelare och talen i den följden är mindre än produkten av de 10^18 första primtalen (vilket natruligtvis är hysteriskt stort).
Tack för svaret! Vad heter satsen som du har beskrivit/vad kan man googla på för att läsa mer? :)
Det är helt enkelt en tillämpning av kinesiska restsatsen
Smutsmunnen skrev:Det är helt enkelt en tillämpning av kinesiska restsatsen
I see! Så pass intressant att jag tycker att den tillämpningen/följden hade förtjänat ett eget namn! :)