Felaktig omskrivning av elnät - varför?
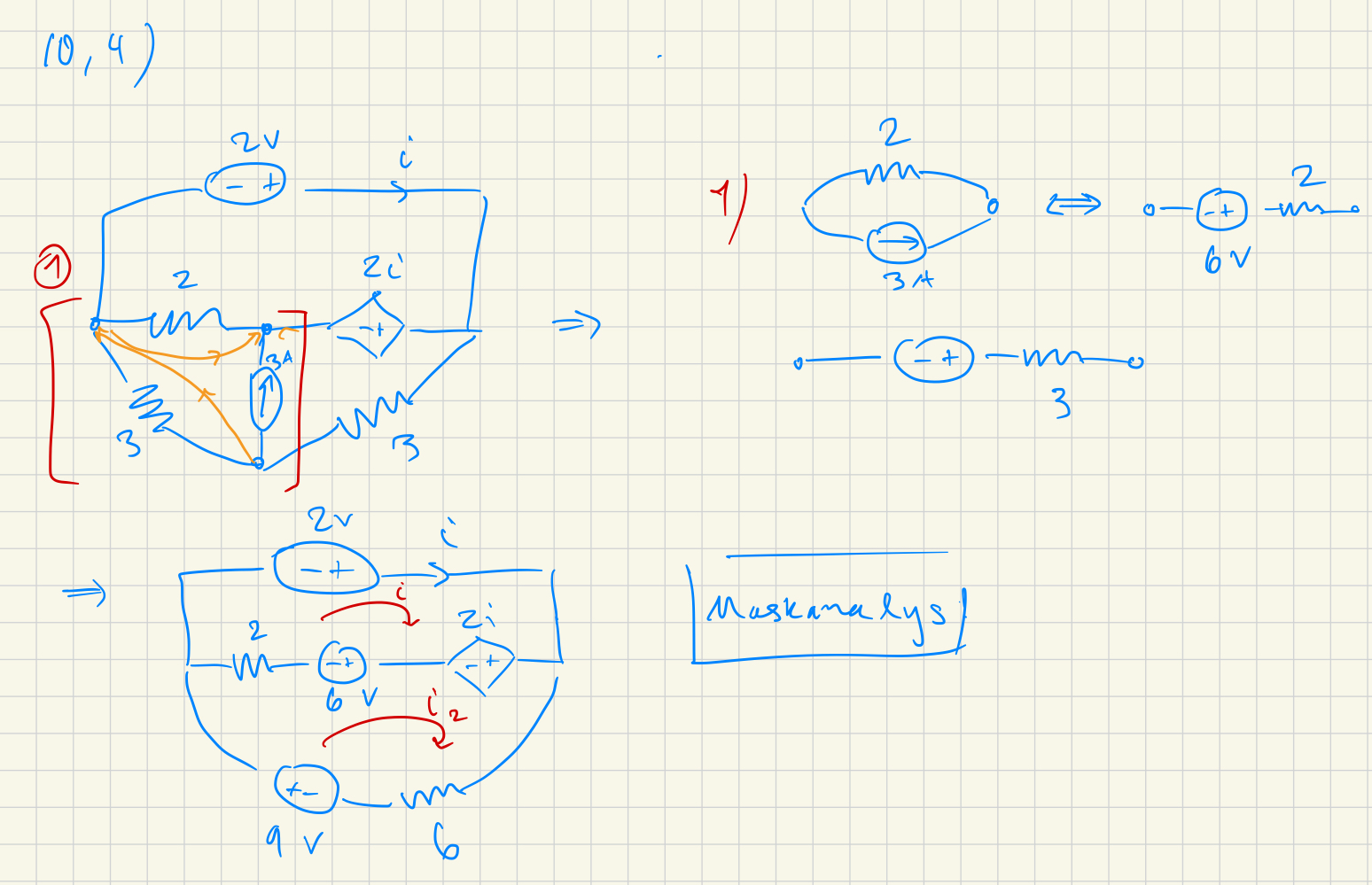
Varför är detta mot reglerna? I facit gör de samma sak fast över motståndet och den beroende spänningskällan till höger.
Och varför kan denna förenkling göras:
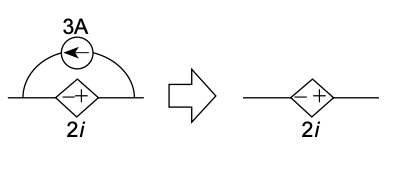
(Har noll kontroll i detta ämne. Mycket känns väldigt random. Det måste vara några fundamentala grejor jag helt missat.)
Andra frågan såg jag var en "lätt" Thevenin-omvandling. Ser man strömkällan som ett motstånd som helt enkelt är 0? Alternativt att strömmen i den fortsatta kretsen endast ges av spänningen som spänningskällan skapat. Strömkällan blir överflödig. Man ser liksom inte punkten där strömmen kommer tillbaka som en nod där det både kommer ström från både ström- och spänningskällan.
Vad skall beräknas i uppgiften?
Ursäkta, det är .
Sägs det i uppgiftstexten att man skall använda Thevenin- eller Norton-omvandlingar?
Nej, det gör det inte.
Eftersom du har en beroende spänningskälla, som beror av en viss ström, brukar det inte funka bra med Thevenin-omvandlingar. Jorda istället den centrala punkten mellan 2 ohms resistansen och 3 A strömkällan och leta efter potentialer och strömmar i kretsen.
Det är inget fel på din första ansats, däremot får du ju se upp lite när du ställer upp maskanalysen eftersom du har en beroende spänningskälla i båda komponenterna av spänningsvektorn.
Jan Ragnar skrev:Eftersom du har en beroende spänningskälla, som beror av en viss ström, brukar det inte funka bra med Thevenin-omvandlingar. Jorda istället den centrala punkten mellan 2 ohms resistansen och 3 A strömkällan och leta efter potentialer och strömmar i kretsen.
Aa, ska kika på’t.
———
Tack D4NIEL. Jag trodde jag var noggrann, men uppenbarligen inte tillräckligt. Återkommer.
D4NIEL skrev:Det är inget fel på din första ansats, däremot får du ju se upp lite när du ställer upp maskanalysen eftersom du har en beroende spänningskälla i båda komponenterna av spänningsvektorn.
Den vill aldrig bli rätt. Snart slänger jag ut min dator genom fönstret.
Vill du vara vänlig att ställa upp matrisekvationen istället...?
I väntan på det kan du testa ett alternativ.

Okej, det funkade bra. Det viktiga verkade vara att när man valt en riktning så följer man den. Stötte på problem när jag räknade ut strömmen i 4 och 6 från varsitt håll. Då blev ekvationerna bara ex
2i-2i+3=3,
vilket inte gav så mycket...hehe.
VI använder din bild och med maskströmmar

Summaresistanserna i de två maskorna ges enligt ditt schema av
, samt
Källspänningsvektorn ges av , . Ekvationssystemet blir:
Men nu har vi den okända strömmen även i källspänningsvektorn. När beroende källor förekommer måste vi modifiera matrisekvationen i ett extra steg. Vi flyttar över termerna med till vänstersidan:
Använd slutligen valfri metod för att lösa ekvationssystemet, t.ex. Cramers regel varvid
Det verkade som att min variant av Cramers regel inte funka så bra. Den gav nämligen alltid fel svar. Nu blev det rätt, tack!



