Felaktigt bevis?

Ja, beviset är faktiskt felaktigt. Olikheterna (17) och (18) gäller ifall $a$ är en (lokal) minimipunkt.

Beviset kan rättas till genom att modifiera de första två raderna enligt följande (ändringarna är rödmarkerade):

Betrakta det fall då $a$ är en ${\color[rgb]{0.8, 0.0, 0.0}\min}$punkt. Fallet då $a$ är ${\color[rgb]{0.8, 0.0, 0.0}\max}$punkt bevisas analogt. Då gäller att $f(x){\color[rgb]{0.8, 0.0, 0.0}\geq} f(a)$ $\forall x \in ({\color[rgb]{0.8, 0.0, 0.0}a} - \delta, {\color[rgb]{0.8, 0.0, 0.0}a}+\delta)$ för något $\delta >0$. Därav följer att ...

Anm: Hade $a$ varit en (lokal) maxpunkt, så gäller $f(x) \le f(a)$ för alla $x$ i en omgivning av punkten $a$ och därmed fås olikheterna (17) och (18) med motsatta olikhetstecken.

Tack för snyggt svar.

Så det jag skrev stämde förutom olikheten mellan f(x) och f(a) ska inte vara strikt?

Precis, och det finns två anledningar:

1) I påståendet sägs ingenting om att maximumet (eller minimumet) skall vara strängt.

2) När man skriver $x \in (a-\delta, a+\delta)$, så tillåter man faktiskt att $x=a$ och därmed kan $f(x) < f(a)$ inte vara sant för varje $x$ i det öppna intervallet $(a-\delta, a+\delta)$ då $f(a)\not<f(a)$

Just det, glömde att fråga. För något delta innebär här, eller kanske alltid, att det räcker man hittar en deltaomgivning där det gäller för alla x? Jag tänker om vi har en lokal extrempunkt så kan funktionsvärdet bli större/mindre än extrempunkten efter ett tillräckligt stort delta. Hur fungerar detta?

Exakt. Man hittar en deltaomgivning. (Omgivningen kan alltid göras mindre, men i allmänhet inte större).

Skrivsättet i ursprungsbeviset, d.v.s.

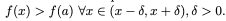
(och även i den modifierade versionen som jag föreslagit) är slarvigt. Vill man vara noggrann, så måste man ta med en till kvantifikator (existenskvantifikatorn då).

Det finns ett positivt tal $\delta$ sådant att det för varje punkt $x$ i $\delta$-omgivningen av $a$ gäller att $f(x) \ge f(a)$.

Symboliskt:

$\exists \delta > 0:\ \forall x \in (a-\delta, a+\delta):\ f(x) \ge f(a)$