Felmeddelande

Determinanten för matrisen är nära noll? Försöker du invertera den eller vad gör du?

Kan du visa din kod, så kanske det är lättare att hjälpa :)

Är ganska krångligt men infogar bilder på allt.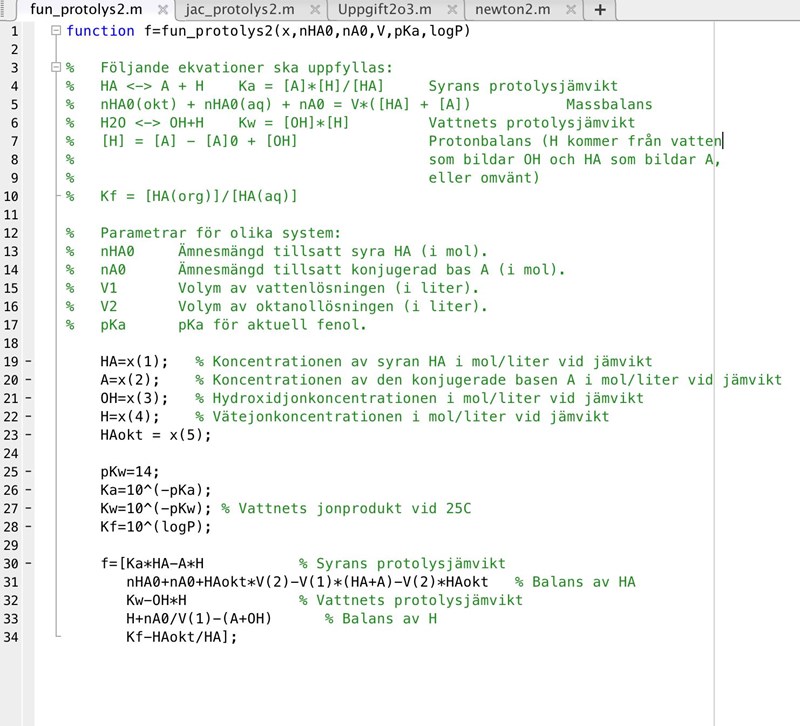

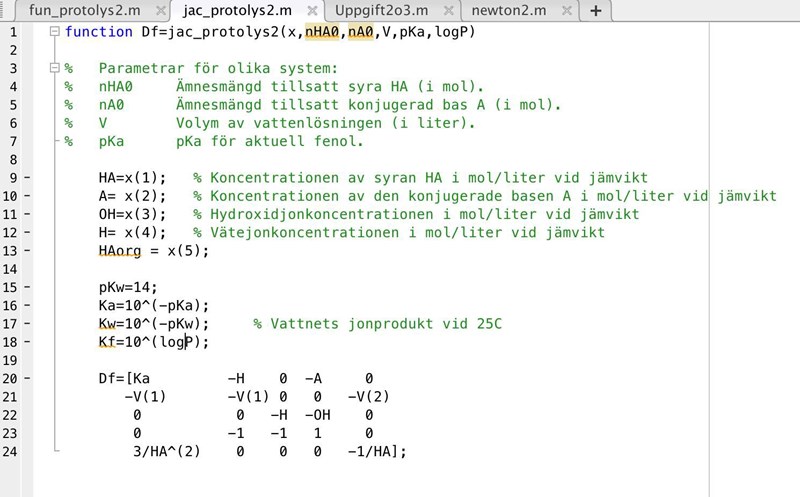
Denna sektion som jag kör: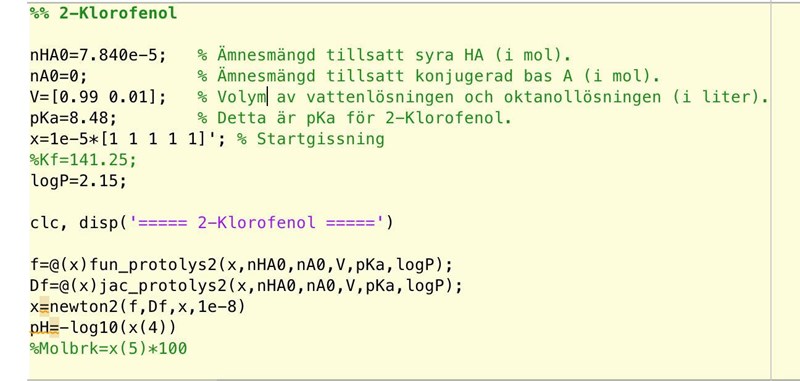

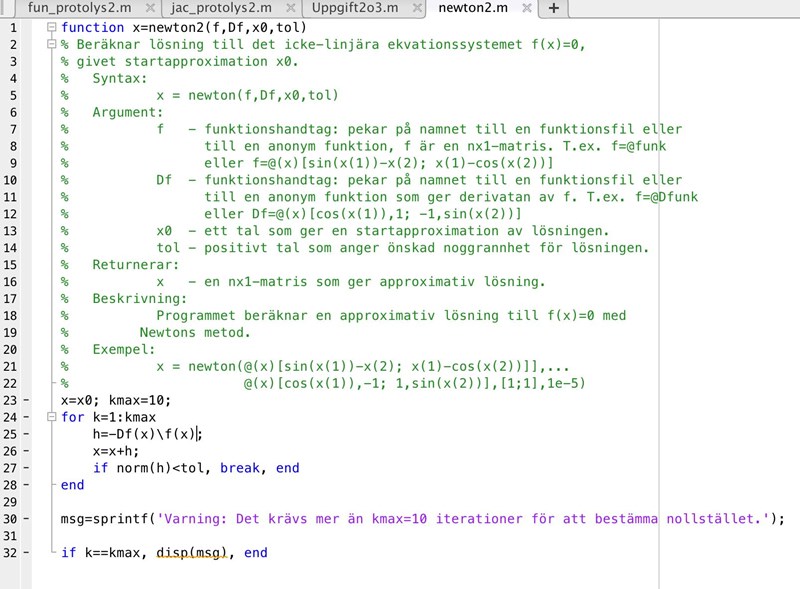
Har fått koden att fungera tidigare, men har lagt till en ekvation nu och det är då det började krångla. Förmodar att det är Newton2 som är problemet då jag även får msg printat efter de andra felmeddelandena. Förstår om det är krångligt att följa, kan förtydliga mer om det behövs.

Hej!

Om $x$ är en startapproximation till det det icke-linjära ekvationssystemet $f(x) = 0$ så ger Newtons metod en ytterligare approximation $x+\delta x$ där uppdateringsvektorn $\delta x$ beräknas som en matrismultiplikation med en invers matris,

    $\delta x = -J(x)^{-1}f(x)$.

Om matrisen $J(x)$ -- som innehåller samtliga första ordeningens partiella derivator till $f$, beräknade i startapproximationen $x$ -- har två eller fler kolonner som är nästan perfekt korrelerade (linjärt beroende) så kommer dess determinant att vara nära noll och matrisens konditionstal att vara mycket högt; det medför att inversen inte kan beräknas ordentligt då den kommer att innehålla enormt stora tal (division med nästan-noll).

Du skulle även kunna pröva att finna minsta-kvadrat-approximationer till uppdateringsvektorn genom att beräkna 

    $\delta x = -(J(x)^{t}J(x))^{-1}J(x)^{t}f(x)$.

Det kan även vara så att du har valt en olämplig startapproximation, $x$, och att ett annat val av $x$ ger dig en matris $J(x)$ som har en determinant som inte är nära noll.

Det känns som att detta kanske är mer av ett kemi-problem då. Provat att ändra approximationen åt olika håll och öka antalet iterationer men får ändå samma felmeddelande samt att "det krävs mer än kmax=... för att bestämma nollstället.

Man brukar undvika att invertera matriser. Man gör hellre en LR-uppdelning eller nåt liknande. Om problenet är inherent numeriskt instabilt hjälper inte det, men jag vet inte om det borde vara så med din uppgift.