2
svar
152
visningar
Fibonaccis talföljd induktionsbevis
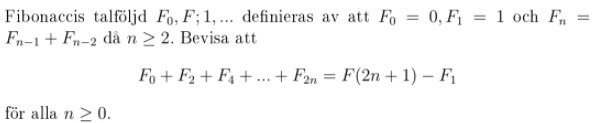
ska man använda stark induktion här?
Behövs inte.
Det står lite dumt. Det man ska bevisa måste vara:
henrikus skrev:Behövs inte.
Det står lite dumt. Det man ska bevisa måste vara:
Skulle induktionsantagandet vara att bevisa
för något ?