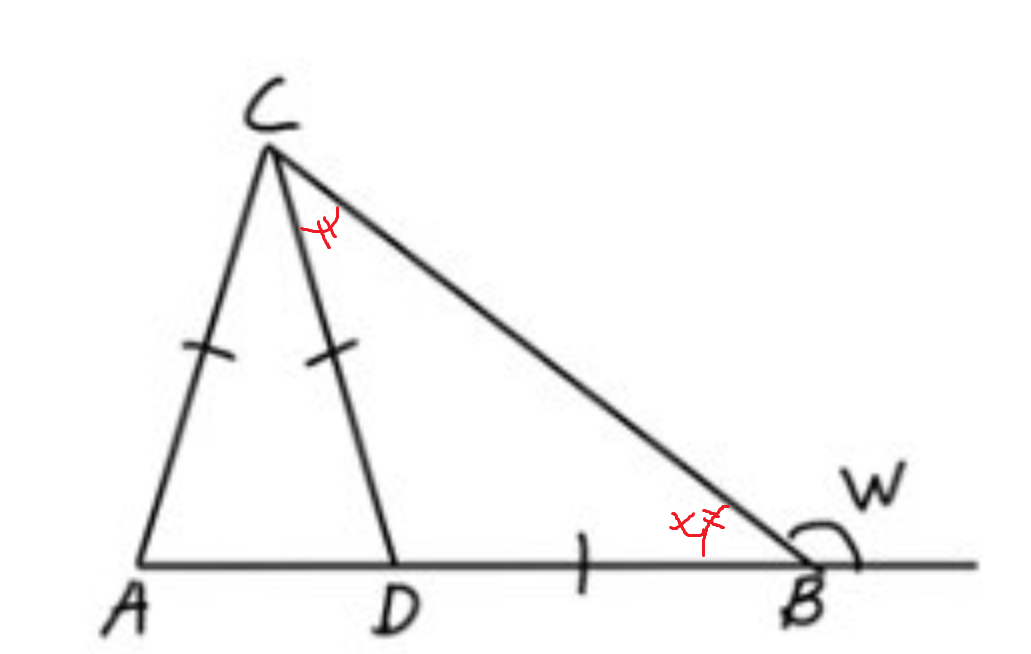
Figur. Visa att vinkeln w = 144 grader.

Hej,
Hade nån kunnat hjälpa mig förstå hur jag hade kunnat lösa en sådan uppgift? Stegvis :)
Hälsningar
Visa spoiler

Nej, jag tycker det är mycket bättre att du försöker själv, steg för steg. När du fastnar så hjälper vi till.
Här kommer en liten puff:
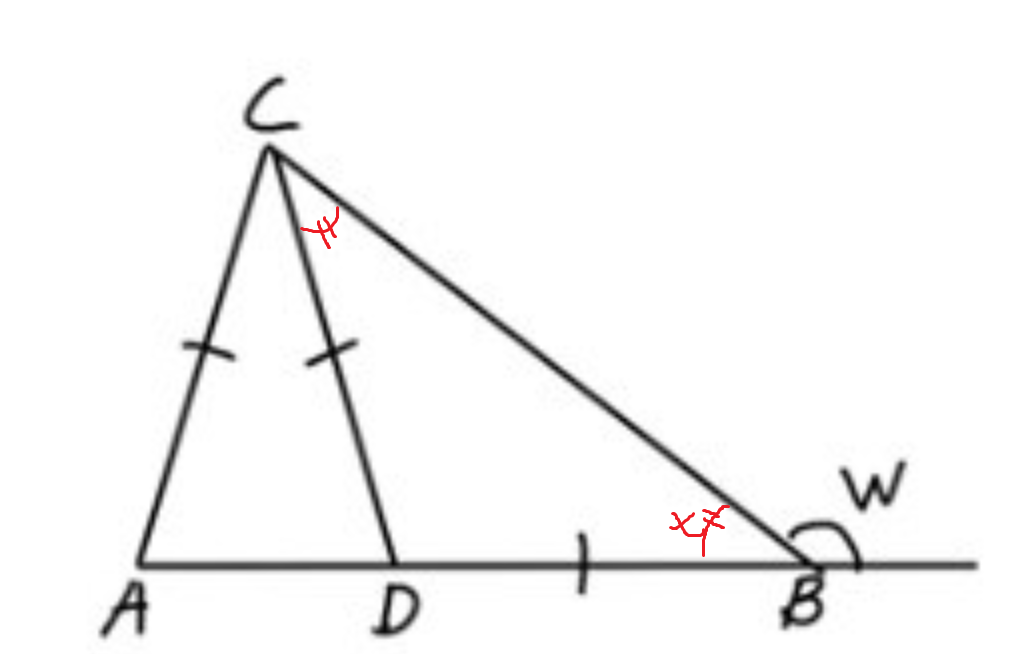
Jag har markerat en vinkel x som du lätt kan räkna ut. Eftersom CD och BD är lika, är BCD likbent. Det ger dig en annan vinkel gratis som jag markerat.
Sedan är det bara att räkna vidare och visa att du får 180 grader som vinkelsumma i alla tre trianglar.
sictransit skrev:Nej, jag tycker det är mycket bättre att du försöker själv, steg för steg. När du fastnar så hjälper vi till.
Här kommer en liten puff:
Jag har markerat en vinkel x som du lätt kan räkna ut. Eftersom CD och BD är lika, är BCD likbent. Det ger dig en annan vinkel gratis som jag markerat.
Sedan är det bara att räkna vidare och visa att du får 180 grader som vinkelsumma i alla tre trianglar.
Hur räknar jag ut x vinkeln?
Trinity2 skrev:Visa spoiler
Hej! Menar du inte att vinkeln DAC är lika med vinkeln BCA, istället för DCA?
flammann skrev:Trinity2 skrev:Visa spoiler
Hej! Menar du inte att vinkeln DAC är lika med vinkeln BCA, istället för DCA?
Jo, det är nog ett skrivfel.
Sådana här uppgifter kan man alltid lösa på olika sätt beroende på vilken väg man tar genom figuren.
Jag började med att kalla vinkel DBC för x.
Vinkel ADC = 2x (yttervinkelsatsen).

5x = 180
x = 36
w = 180 - 36 = 144
Louis skrev:Sådana här uppgifter kan man alltid lösa på olika sätt beroende på vilken väg man tar genom figuren.
Jag började med att kalla vinkel DBC för x.
Vinkel ADC = 2x (yttervinkelsatsen).
5x = 180
x = 36
w = 180 - 36 = 144
Det är en fin lösning!
När jag ser på dessa uppgifter med äldre ögon, och börjar fundera på exakt var i min utbildning hag hade nytta av detta, kommer jag fram till svaret: Absolut ingenstans. Man kan ställa sig frågan om de gamla grekerna hade harvat geometri till leda om Newton et al. hade fötts 400 BC… Hörmander framhöll att geometri är av yttersta vikt, men man kan undra vilken nivå han menade.
Det var väl en sådan diskussion här på PA för någon tid sedan. Om nyttan av geometri. Du kanske var inblandad. Jag minns inte var den landade. Om den landade.
Louis skrev:Det var väl en sådan diskussion här på PA för någon tid sedan. Om nyttan av geometri. Du kanske var inblandad. Jag minns inte var den landade. Om den landade.
Kanske den landade i att det var en spegling av tiden? Jag kommer ej ihåg diskussionen själv. Matematik revideras löpande i läroböcker men vissa moment verkar bestå.
Louis skrev:Sådana här uppgifter kan man alltid lösa på olika sätt beroende på vilken väg man tar genom figuren.
Jag började med att kalla vinkel DBC för x.
Vinkel ADC = 2x (yttervinkelsatsen).
5x = 180
x = 36
w = 180 - 36 = 144
Hej!
Hade du kunnat förklara mer om hur du gjorde :)
Antag att vinkel DBC=x.
Vinkel BCD = x (likbenthet)
Vinkel ADC = 2x (yttervinkelsatsen)
Vinkel DAC = 2x (likbenthet)
Vinkel ACB = 2x (likbenthet)
x + 2x + 2x = 180
x = 36
w = 180 - 36 = 144