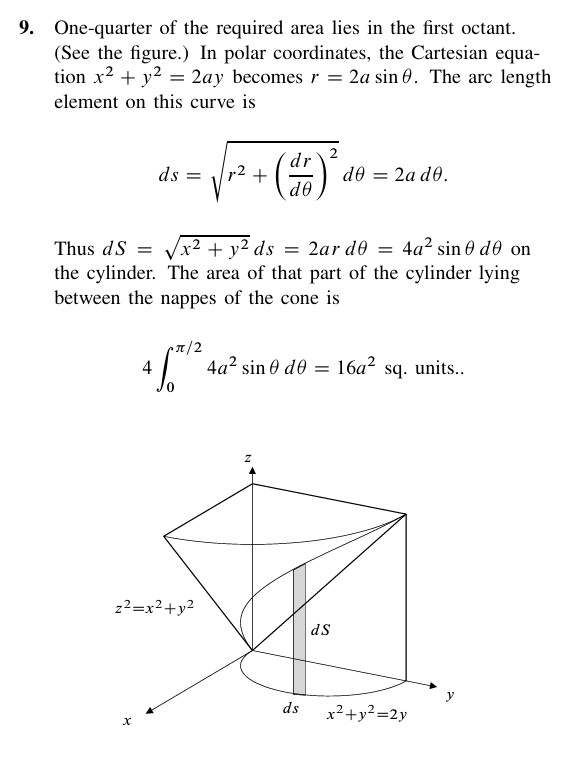
Find the area of the part of the cylinder that lies outside the cone

Hej! Jag har några frågor till lösningen på denna fråga.

1.Hur visste de hur de skulle rita upp figuren? När jag såg ekvationerna tänkte jag att cylindern hade radien sqr(2ay) och att den har centrum i origo. Hur visste de att dess centrum skulle vara på den positiva sidan av y-axeln?

2.De säger att $x^{2} + y^{2} = 2 a y$ ger att $r = 2 a \sin (θ)$ men är inte $x^{2} + y^{2} = r^{2}$ ? så Det borde bli att $r = \sqrt{2 a \sin (θ)}$ ?

Tack på förhand!

Cirkelns ekvation är x² + y² = R², där R är radien (en konstant). Men i vår ekvation så är HL inte en konstant, utan beror av y.

1. Använd kvadratkomplettering.

x² + y² - 2ay = 0.

x² + (y-a)² - a² = 0.

x² + (y-a)² = a², dvs en cirkel med radie a med centrum i (0, a).

2. r² = x² + y² = 2ay = 2arsin $θ$

r = 2asin $θ$ .

PATENTERAMERA skrev:
Cirkelns ekvation är x² + y² = R², där R är radien (en konstant). Men i vår ekvation så är HL inte en konstant, utan beror av y.

1. Använd kvadratkomplettering.

x² + y² - 2ay = 0.

x² + (y-a)² - a² = 0.

x² + (y-a)² = a², dvs en cirkel med radie a med centrum i (0, a).

2. r² = x² + y² = 2ay = 2arsin $θ$

r = 2asin $θ$ .

Tack för svar! juste glömde bort att y blir ju inte bara sin(theta) utan rsin(theta) tack!:)

Svara