Find the area of the part of the plane Ax+By+Cz = D

Hej! jag förstår inte riktigt hur de gjort i facit på denna uppgift? varför tar de normalvektorn dividerat med normalvektorn dotproduct med zeta?

Under föreläsningarna har man beräknat areaelementet genom att parametrisera och sedan beräkna normalen av riktningsvektorn deriverad med avseende på dess parametrar (dr/d(theta) $\times$ dy/d(theta) .

Facit:

Min början på lösning:

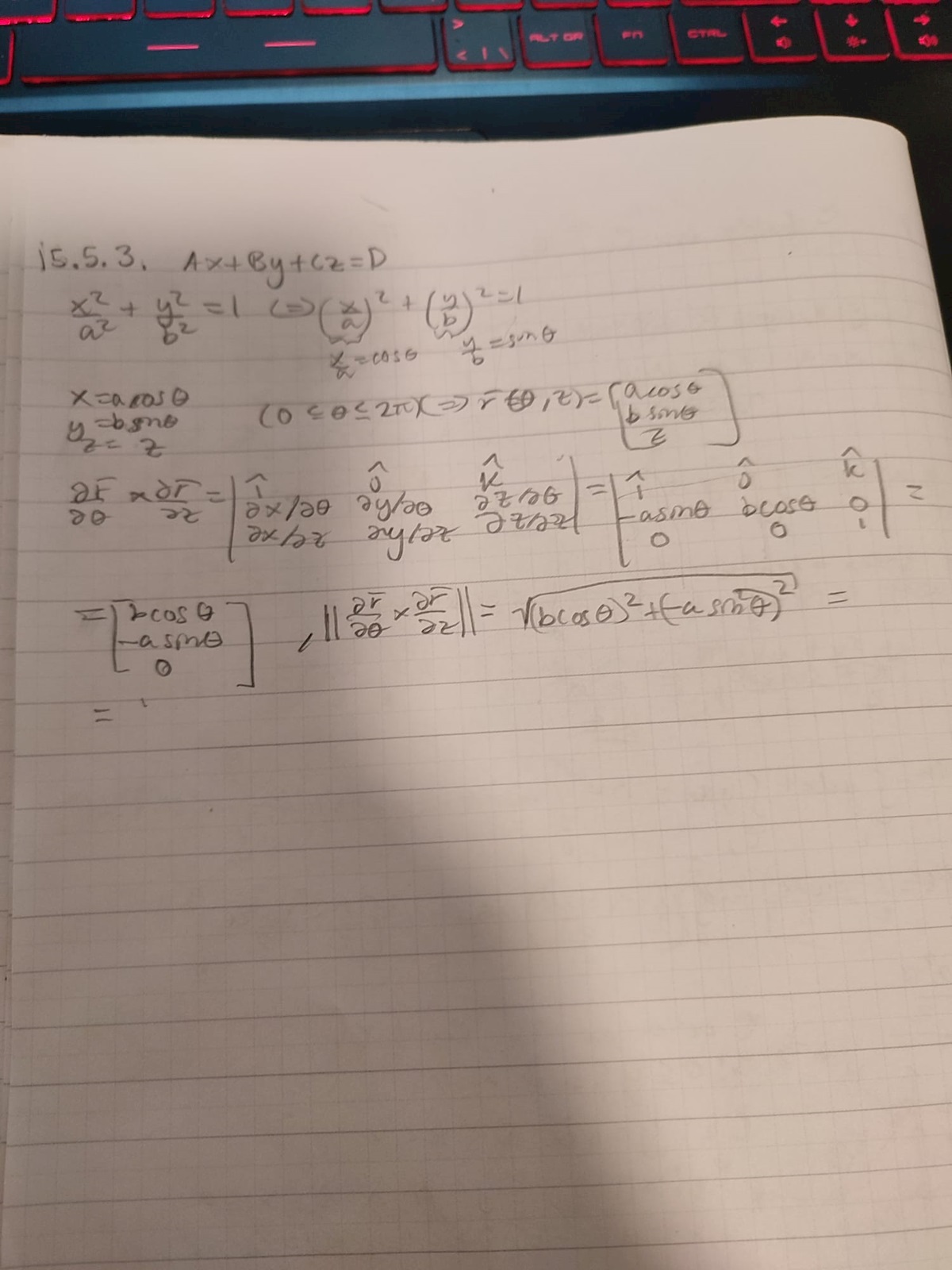
Tack på förhand!

Jag tycker det blir lättare om man skalar bort en dimension.

Kolla om min bild ger något, här bestämmer jag längdelementet med en analog formel.

Marilyn skrev:
Jag tycker det blir lättare om man skalar bort en dimension.

Kolla om min bild ger något, här bestämmer jag längdelementet med en analog formel.

Tack för svar! Jag förstår dock tyvärr inte bilden riktigt. Är $(\frac{A}{B})$ normalvektorn till planet?

Ja, för hand tycker jag kolonnvektorer är tydligare än Ai + Bj.

Fast jag skalade ner till att beräkna ett längdelement på en linje i stället för ett ytelement på ett plan.

Och det är såklart inte A genom B, utan vektorn.

Marilyn skrev:
Ja, för hand tycker jag kolonnvektorer är tydligare än Ai + Bj.

Fast jag skalade ner till att beräkna ett längdelement på en linje i stället för ett ytelement på ett plan.

Och det är såklart inte A genom B, utan vektorn.

ah okej! Men varför blir längden $\frac{\sqrt{A^{2} + B^{2}}}{| [\begin{matrix} A \\ B \end{matrix}] d o t [\begin{matrix} 0 \\ 1 \end{matrix}] |}$ ?

Vi har en stor triangel med (A²+B²)^1/2 som hypotenusa, och en likformig triangel med l som motsvarande sträcka.
|B| skalas ned till 1, då skalas hypotenusan också ned med en faktor 1/|B|.

Marilyn skrev:
Vi har en stor triangel med (A²+B²)^1/2 som hypotenusa, och en likformig triangel med l som motsvarande sträcka.
|B| skalas ned till 1, då skalas hypotenusan också ned med en faktor 1/|B|.

Ah okej! Men varför skalar man ned B till 1?

Svara

Visa senaste svar