Find the flux of F = xi + zj
Hej! Jag försöker lösa denna uppgift och försöker följa hur de gjort i exemplena i föreläsningarna där de först beräknade ytelementet och sedan andvände det för att beräkna arean. Jag vet dock inte vad jag gör fel? och förstår inte riktigt hur de gjort i facti, är normalvektorn till de olika ytorna? och varför får de de till -i,-j och -k?
Tack på förhand!

Min lösning:
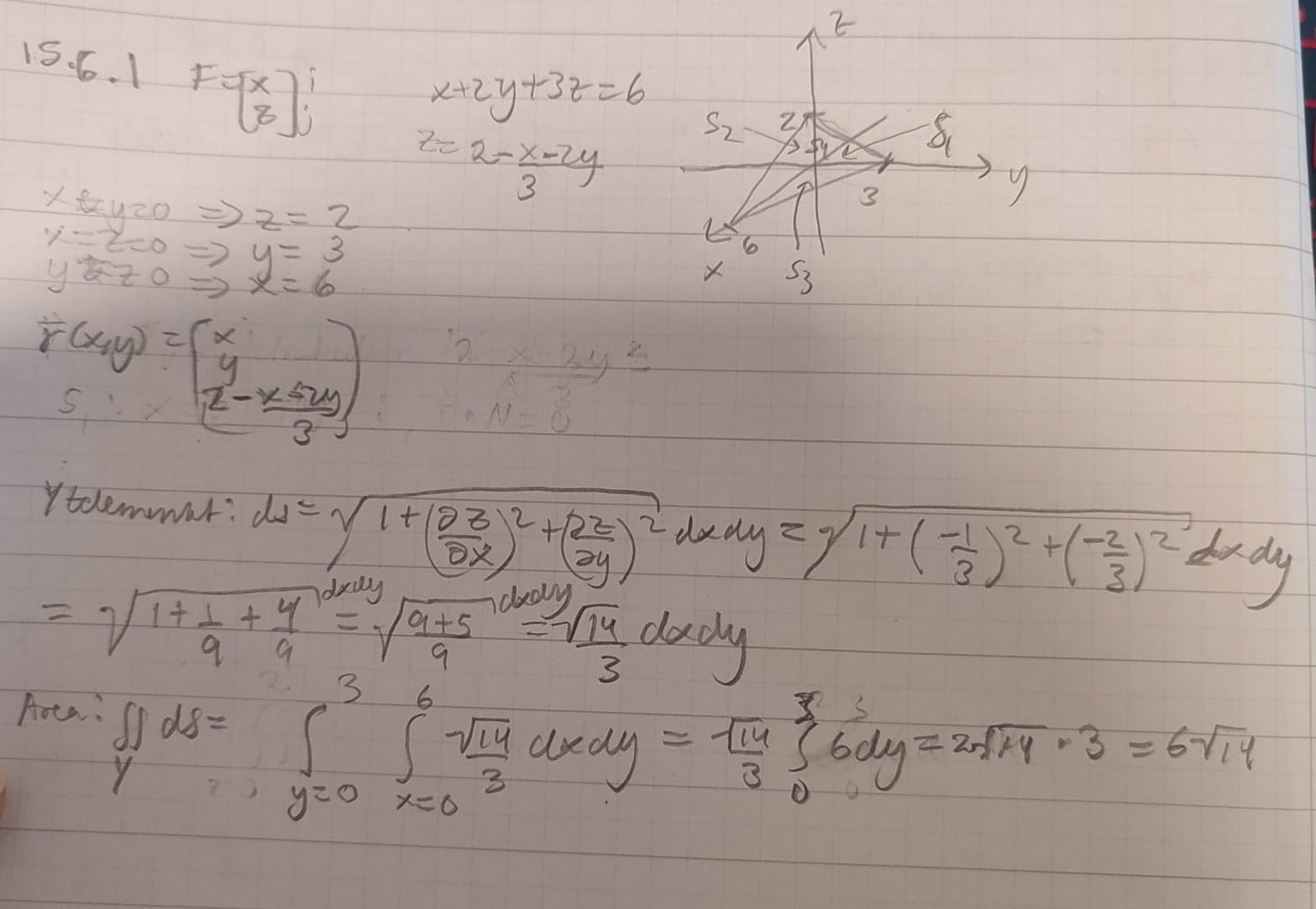
Facit:


Jag tror du blandar ihop några koncept.
Du har tagit fram en parametrisering av ytan som bildar ett "tak" över ett triangelområde i xy-planet. Den stämmer förutom att det ska vara ett plustecken mellan och .
Sedan beräknar du arean av den triangelytan men glömmer att basytan (parameterområdet) också är ett triangelområde. Det korrekta uttrycket för just den arean är egentligen
Men det är inte arean du ska beräkna, utan flödet genom ytan som ges av
Fältet är vilket med din parametrisering alltså blir
Normalen till ytan blir
I facit har de räknat med enhetsnormalen, och du får naturligtvis normera den om du vill, men skilj alltså på och . Du måste då multiplicera med normen på slutet, förmodligen har ni färdiga formler för det.
Vi räknar ut skalärprodukten
Flödet ut från just den delytan blir alltså
Jag vill slutligen nämna att den här uppgiften blir mycket enklare med Gauss divergenssats. Volymen av en pyramid ges som bekant av basytan gånger höjden genom tre och blir i vårt fall ). Divergensen av fältet är . Alltså blir det totala utflödet bara volymen av tetradern:
(Mycket enklare än att räkna ut normaler för varje delyta osv...)

