Finn alla reella lösningar till ekvationen

Cos^2 x är lika med 1 - sin^2x 

Ser ut som du har gjort fel där

ItzErre skrev:

Cos^2 x är lika med 1 - sin^2x 

Ser ut som du har gjort fel där

Mahiya99 skrev:

ItzErre skrev:

Cos^2 x är lika med 1 - sin^2x 

Ser ut som du har gjort fel där

Vad händer mellan rad två och tre? Använder du dubbla vinkeln för cosinus? Det är nog bättre att använda dig av trigonometriska ettan. Dubbla vinkeln ger $\cos{(2x)}$, inte $\cos^2{(x)}$. :)

$$\begin{gathered} 2{\cos }^2\left(x\right)-1=\sin \left(x\right) \\ 2(1-{\sin }^2\left(x\right))-1=\sin \left(x\right) \\ 2-2{\sin }^2\left(x\right)-1=\sin \left(x\right) \end{gathered}$$

Nu kan du sätta $t=\sin{(x)}$. :)

Jag får dessa lösningar. Dock har facit redovisat sin lösning på annat sätt så jag vet ej om min lösning är godkänd? 

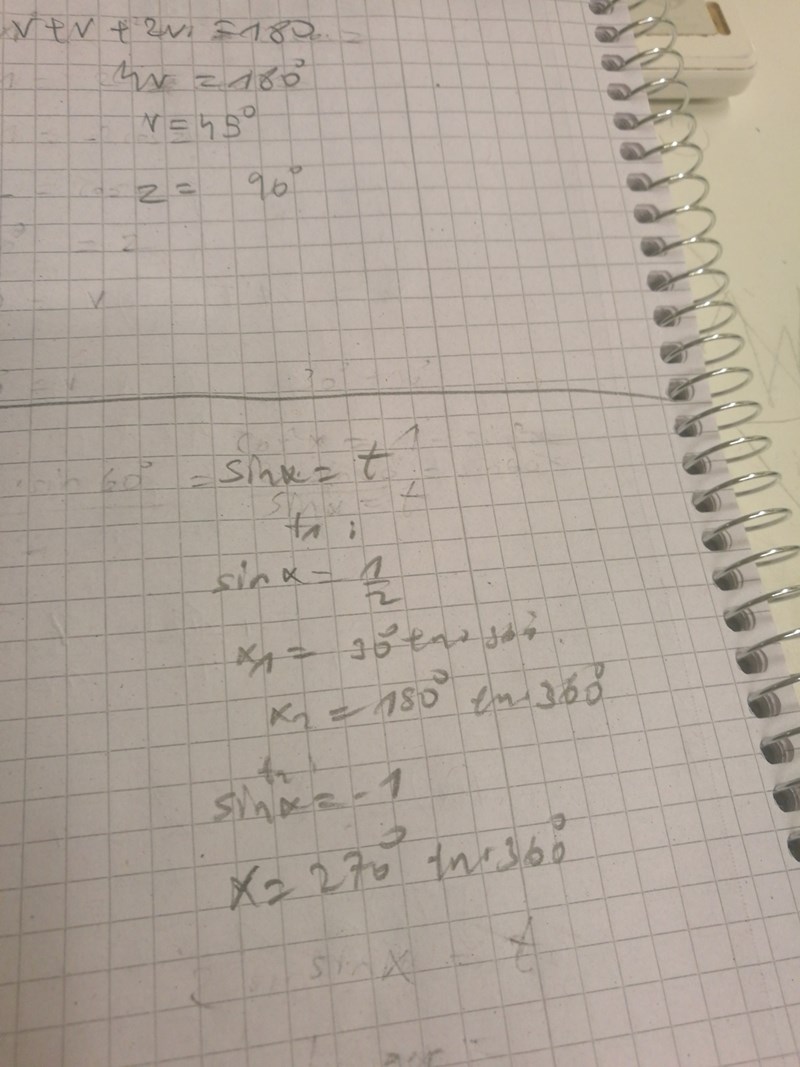
Rita in dina lösningar i enhetscirkeln. Rita in facits lösningar i enhetscirkeln. Jämför.

Här byter du rst ett minustecken mot ett plustecken.

Sedan byter du tillbaka från ett plustecken till ett minustecken.

Yngve skrev:

Här byter du rst ett minustecken mot ett plustecken.

Sedan byter du tillbaka från ett plustecken till ett minustecken.

Smaragdalena skrev:

Rita in dina lösningar i enhetscirkeln. Rita in facits lösningar i enhetscirkeln. Jämför.

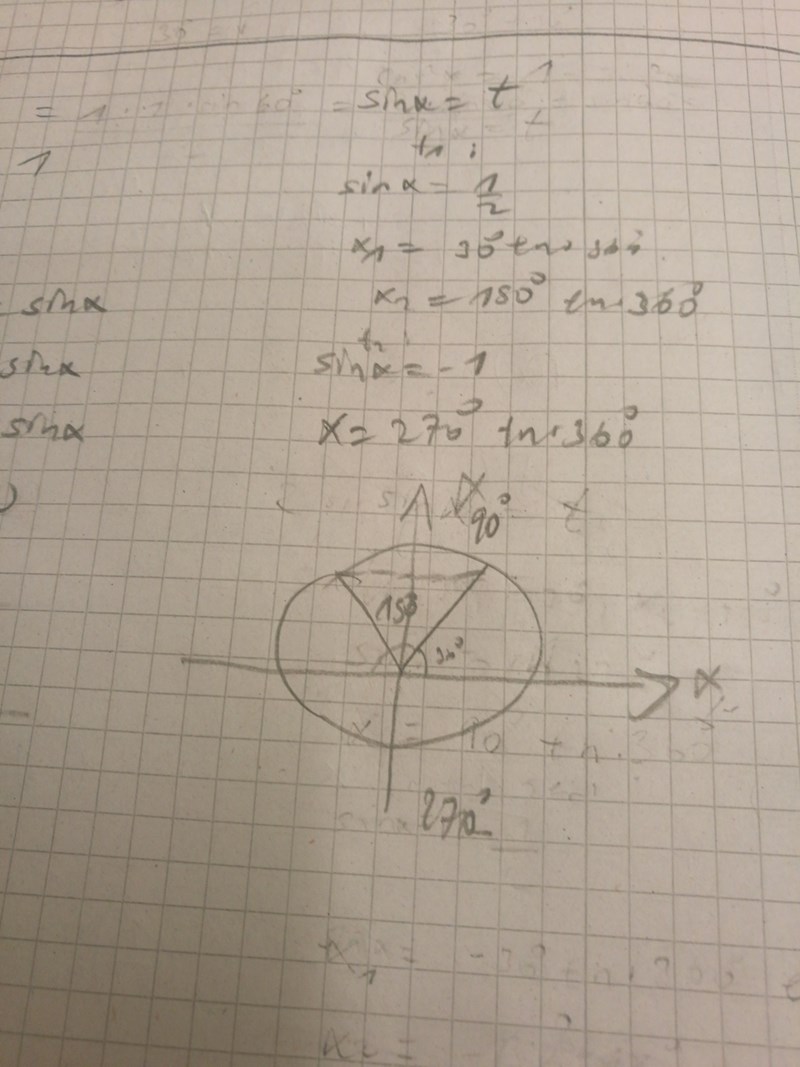
Mahiya99 skrev:

Det är fortfarande två fel (som tar ut varandra).

Yngve skrev:

Mahiya99 skrev:

Det är fortfarande två fel (som tar ut varandra).

Hur ska det se ut då? 

Ser du felen? Jag har markerat dem i ett tidigare svar.

Yngve skrev:

Ser du felen? Jag har markerat dem i ett tidigare svar.

Aa

Men då får jag istället

2-2sin^2x-1-sinx=0

Ja det är rätt.

Yngve skrev:

Ja det är rätt.

Ok jag fick tre lösningar x1=30, x2 =150 och x3=270 grader 

Bra. Och alla ska ha en periodicitet på 360°.

Yngve skrev:

Bra. Och alla ska ha en periodicitet på 360°.

Yes. Jag svarade x1=30+n*360, x2=150+n*360 och x3= 270+n*360

Facit

Jag undrar om man ska svara som dem eller om mitt svar där jag gav tre lösningar ses ok? 

Lösningarna i facit är angivna i radianer och dina är angivna i grader, men de beskriver samma lösningsmängder. Så ditt svar borde vara OK.

Yngve skrev:

Lösningarna i facit är angivna i radianer och dina är angivna i grader, men de beskriver samma lösningsmängder. Så ditt svar borde vara OK.

Ja precis