Finn Maclaurinutvecklingen..

.. av ordning 4 av funktionen $f (x) = e^{2 x} \cos x$

Blir osäker hur man gör när jag ska multiplicera ihop utvecklingarna för $e^{2 x} & \cos x$ . Tänkte att jag borde multiplicera allt som ger x^4 termer (eller mindre), och sätta det som blir av högre grad till x^5*B(X)

Jämförde min utveckling med f(x) (https://www.desmos.com/calculator/obcba7z9lc) och tyckte den såg OK ut..

Men facit håller inte med mig, hur borde jag tänka vid parantesmultiplikationen ? Eller har jag räknat fel någonstans?

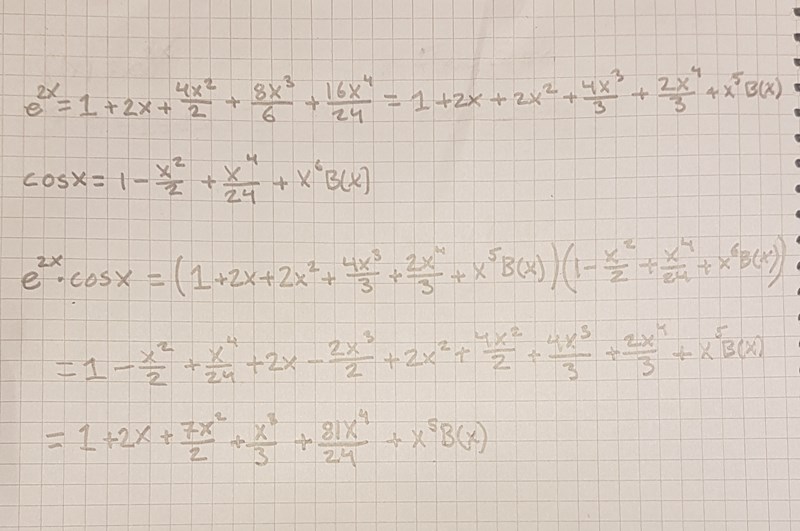
Någonting har blivit fel när du multiplicerar 2x^2 från den vänstra parentesen.

parveln skrev:
Någonting har blivit fel när du multiplicerar 2x^2 från den vänstra parentesen.

Tack! Sitter på bussen just nu ska kika när jag kmr hem. Men i övrigt resonerar jag korret hur man löser den här typen av uppgifter ?

Alternativt utvecklar man det enligt:

$e^{2x}\cos x = e^{2x}\Re (e^{ix})=\Re (e^{(2+i)x})=$

$\Re ( 1+(2+i)x+\frac{(2+i)^2}{2!}x^2+...+\frac{(2+i)^n}{n!}x^n)=...$

poijjan skrev:
parveln skrev:
Någonting har blivit fel när du multiplicerar 2x^2 från den vänstra parentesen.
Tack! Sitter på bussen just nu ska kika när jag kmr hem. Men i övrigt resonerar jag korret hur man löser den här typen av uppgifter ?

Ja, det går att göra så.

Svara

Visa senaste svar