Finns det sådana mängder A, B och C? (Klurig uppgift)
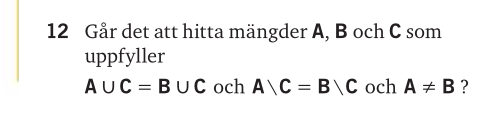
Facit:
Visa spoiler
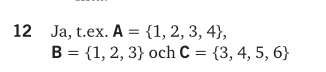
Jag har nu stött på denna uppgift (och en del liknande) och jag vet aldrig hur jag ska börja? Ska jag ansätta A, B och C till godtyckliga mängder och sedan fortsätta därifrån? Då kommer jag inte långt. Hur kan jag på bästa sätt "approacha" en sådan här uppgift?
Man kan börja med den första likheten. Den säger att av elementen i C är "de som tillhör även A" och "de som tillhör även B" exakt samma element.
C innehåller alltså inget element som är "C och A men inte B", inget element som är "C och B men inte A".
Slarvigt uttryckt: Om du bara letar inom C, så ser A och B likadana ut.
Skulle du kunna visa med ett exempel?
A = alla schackspelare
B = alla vänsterhänta
C = alla som bor i Ankeborg
Om det nu är så att bara Kalle Anka och Musse Pigg är vänsterhänta, och alla andra högerhänta, så kan det också vara så att bara de två i Ankeborg spelar schack. Utanför Ankeborg finns det såklart många andra vänsterhänta, och många andra schackspelare, men
unionen av A och C är Kalle och Musse.
unionen av B och C är Kalle och Musse
Jag ritade ett Venn-diagram. Sedan för att få A union B = B union C så markerade jag två regioner gråa, för att de måste vara tomma. Efter det konstaterade jag att A\C redan var B\C, så då är jag klar. Om man vill ha exempel kan man lägga siffror i A, B och C så att det stämmer.


