Fixpunktmetoden
Uppgiften är att man ska lösa e^(-x) = 2x för x0=3 och även testa med x0=-5.
I facit står det att man kan inte garantera att metoden fungerar för att |g'(-5)| >1 men hur ser man det??? g(x) är rätta linjen y=x och när jag plottar det så ser jag att den har lutning 1 för både om x0=0,3 eller x0= -5. 
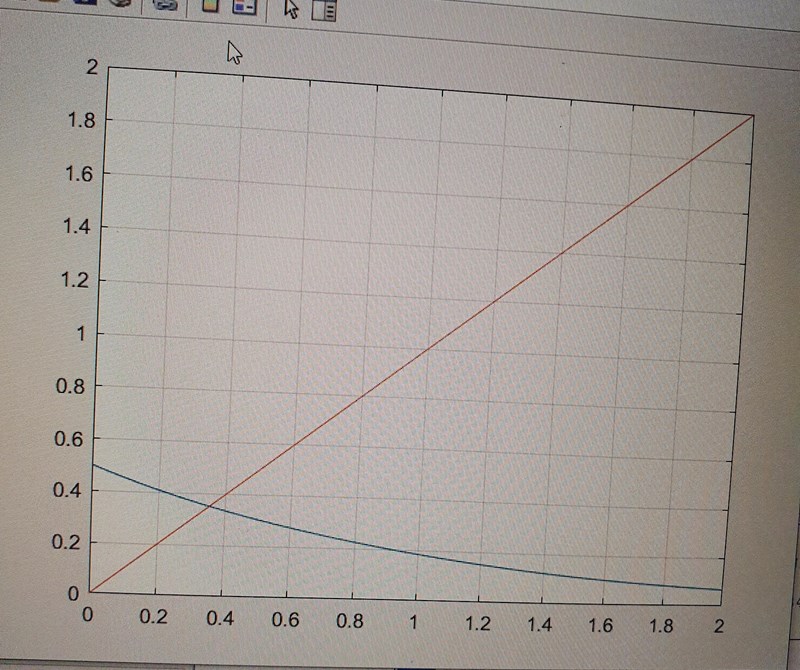
g(x) ser ut att vara (e-x)/2.
Aha nej. Förlåt det blev fel. I koden som jag skrev g(x) är lätta linjen x=y
Men asså fortfarande. Den blåa linjen är exponentiela funktione n och oavsätt om jag sätter x0 till -5 eller 0.3 så har den lutning som är mindre än noll.
I am Me skrev:Uppgiften är att man ska lösa e^(-x) = 2x för x0=3 och även testa med x0=-5.
I facit står det att man kan inte garantera att metoden fungerar för att |g'(-5)| >1 men hur ser man det??? g(x) är rätta linjen y=x och när jag plottar det så ser jag att den har lutning 1 för både om x0=0,3 eller x0= -5.
Till exempel här satte jag x0= 0.5 och lutningen nära skärningspunkten är mindre än noll.
Din fråga verkar inte vara samma som från början. Vad är din fråga nu?
Laguna skrev:Din fråga verkar inte vara samma som från början. Vad är din fråga nu?
Min fråga är att drivatan för den blåa linjen alltså . Varför skriver de i facit att |g'(-5)|>1 och |g'(x)| <1 ??
Absolutbeloppet av derivatan är positivt.
ja men absolutbelopp är alltid positiv.
Ja, så vad är fel med det facit säger?


