Fjäder–massa-system: Villkor för att en bricka inte ska tappa kontakten

Fjädern ser inte så kraftig ut, men det står att den är det. Tanken är att fjädern kan trycka ner vikten med större acceleration än tyngdaccelerationen, och då lämnar den brickan bakom sig.

Hur menar du? Förstår inte riktigt. 

Vad står det i facit?

Jag tycker det som Laguna säger verkar vettigt.

Accelerationen är a = ${\omega }^{2}A\sin \left(\omega t\right)$. A = amplituden.

Newtons andra för brickan: N - mg = ma. m är brickans massa. Normalkraften N kan inte bli negativ (riktad nedåt).

N = m(g + a) $\ge$ 0 => g + a $\ge$ 0 => g - ${\omega }^{2}A$ $\ge$ 0 => g $\ge$ $\frac{k}{M}A$ => k$\le \frac{gM}{A}$. M är viktens massa - brickans massa är försumbar i sammanhanget.

För mig hade det underlättat att lösa frågan om jag vet vilka krafter som verkar på brickan i alla tre fallen. PATENTERAMERA skriver N för normalkraften antar jag, men brickans massa är försumbar så vilket föremål tillhör normalkraften? Både Laguna och PATENTERAMERA skriver något om accelerationerna, jag tänker mer på specifika krafter i sammanhanget

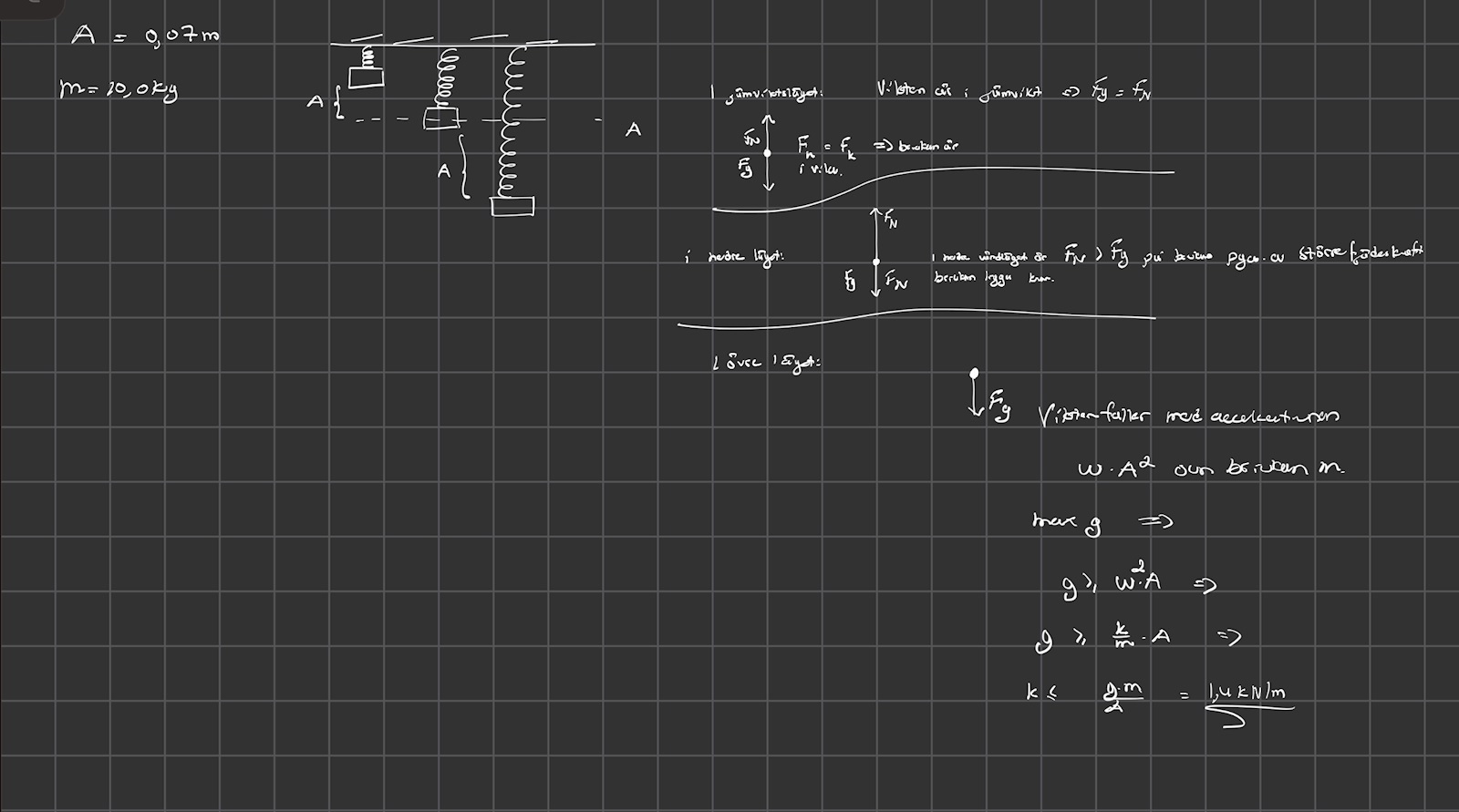
Min uträkning. Jag har nu använts både viktens massa och dess normalkraft för att lösa uppgiften eftersom det måste vara dessa som påverkar brickan? Men varför vet jag inte. Tänker jag rätt?

Jag är lite förvirrad nu. I övre vändläget så påverkas väl vikten av två nedåtriktade krafter: tyngdkraften och kraften från fjädern. Är då inte accelerationen nedåt alltid större än g?

Anonym_15 skrev:

För mig hade det underlättat att lösa frågan om jag vet vilka krafter som verkar på brickan i alla tre fallen. PATENTERAMERA skriver N för normalkraften antar jag, men brickans massa är försumbar så vilket föremål tillhör normalkraften? Både Laguna och PATENTERAMERA skriver något om accelerationerna, jag tänker mer på specifika krafter i sammanhanget

N är normalkraften från vikten på brickan. Brickan påverkas av N och tyngdkraft.

Laguna skrev:

Jag är lite förvirrad nu. I övre vändläget så påverkas väl vikten av två nedåtriktade krafter: tyngdkraften och kraften från fjädern. Är då inte accelerationen nedåt alltid större än g?

Inte nödvändigtvis. Amplituden kan vara så liten att fjädern inte når upp till sin ospända längd.

Rent generellt så gäller att den resulterande kraften (fjäder + tyngd) är -ky, där y är avvikelsen från jämviktsläget.

Alltså tänker jag rätt angående dem vikter som verkar på brickan: endast normalkraft och tyngdkraft från vikten? Vikten å andra sidan påverkas av en spännkraft.

Krafter på brickan: normalkraft från vikten och tyngdkraft.

Krafter på vikten: fjäderkraft, tyngdkraft och normalkraft från brickan (denna sista kraft kan försummas i sammanhanget).

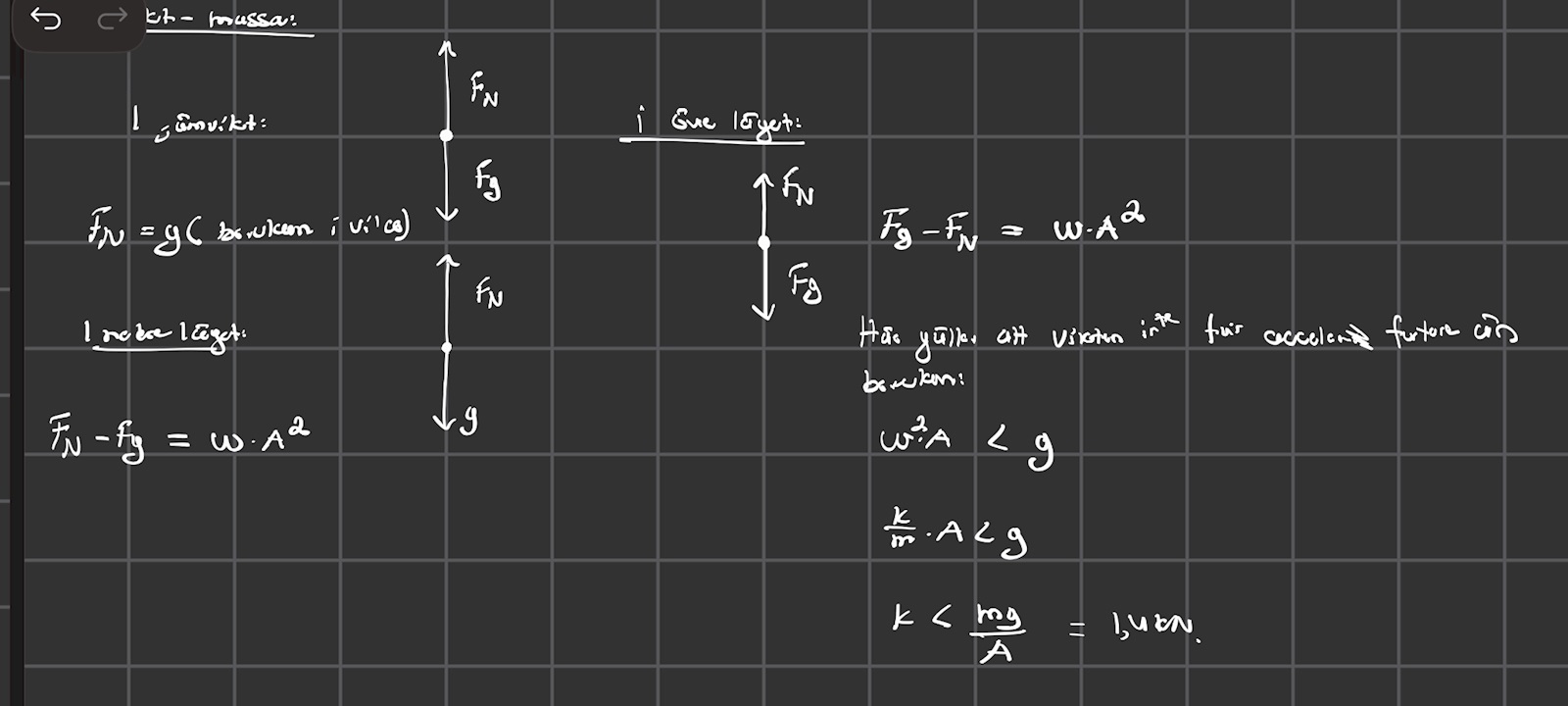Nytt försök. Men fortfarande klarnar det inte till. Normalkraften, hur stor är den? Viktens massa eller brickans egen massa? 

I övre vänteläge måste Fg - N > wˆ2 * A. Men eftersom brickans massa skulle försummas kommer väl även Fg att försummas och därefter N också?

Kalla brickans massa m och viktens massa M.

Då är ${\omega }^2=\frac{k}{m+M}\approx \frac{k}{M}$. Här försummar vi brickans massa som är mycket mindre än viktens massa.

Sedan sätter vi upp rörelseekvationen för brickan i högsta läget. Neråt som positiv riktning.

mg - F_N = m${\omega }^{2}A$. Sedan så måste F_N vara större än eller lika med noll, annars tappar brickan kontakten med vikten.

m(g-${\omega }^{2}A$)$\ge$0.