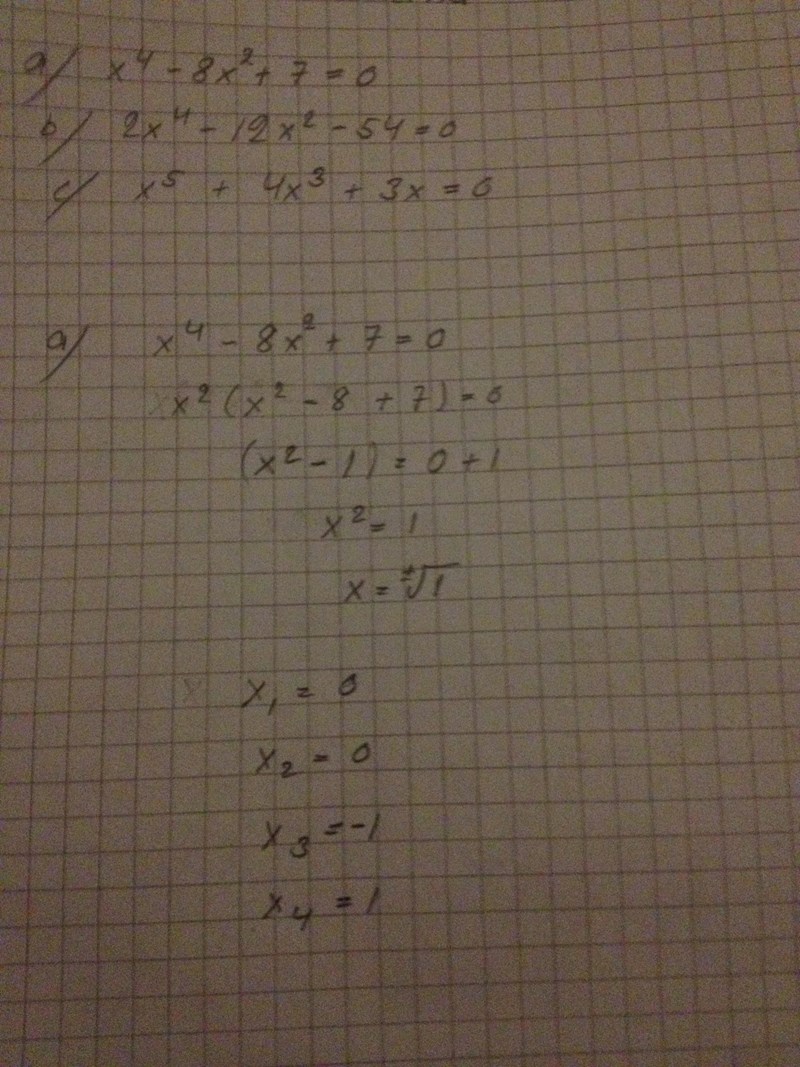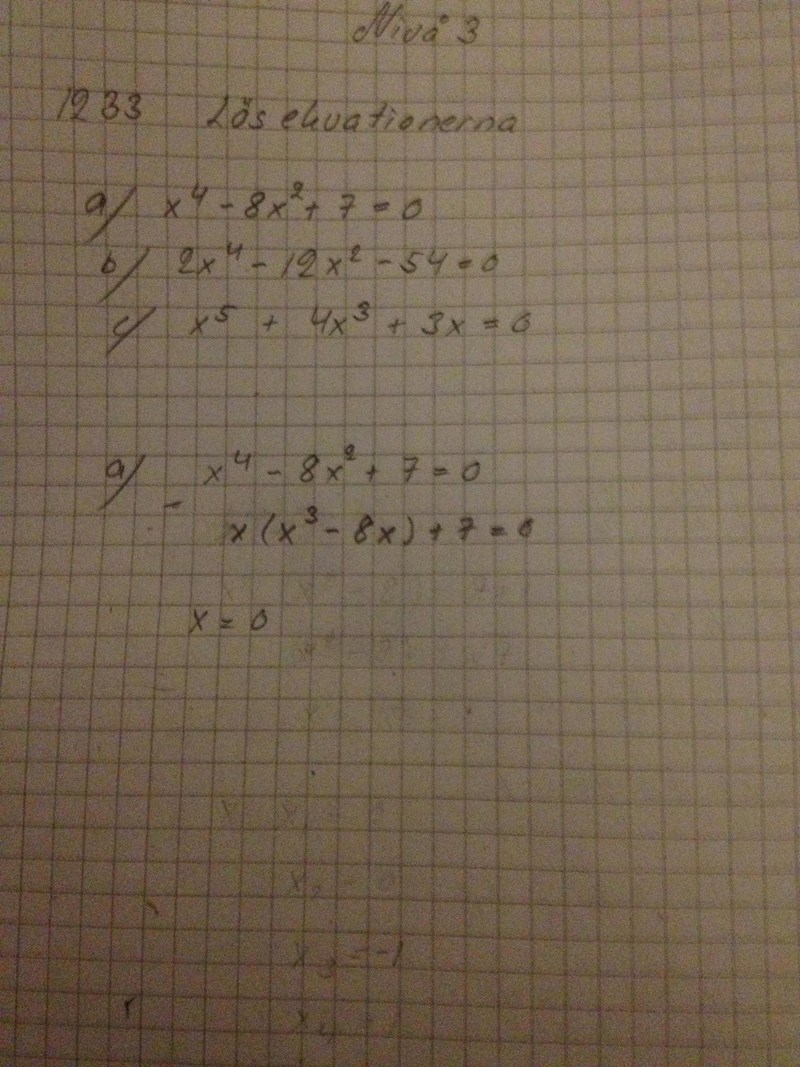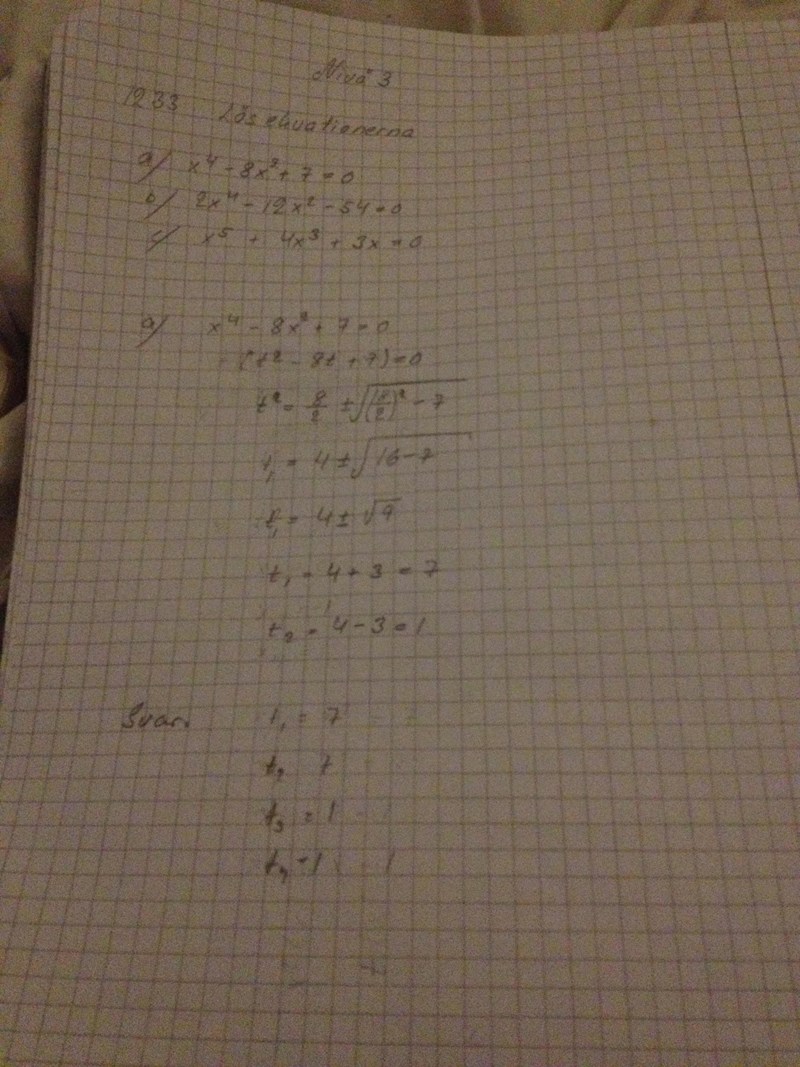Fjärde grads ekvation (Matematik/Matte 3/Algebraiska uttryck)

Hmm... vad händer på andra raden? $x^{2} (x^{2} - 8 + 7) = x^{4} - 8 x^{2} + 7 x^{2}$ det är inte din ursprungliga ekvation.

Det du kan göra är att göra en variabelsubstitution vi säger att $x^{2} = t$ hur ser ekvationen ut då? om vi ersätter $x^{2}$ med $t$ ?

$x^{2}$ är inte en gemensam faktor till alla termer i vänsterledet, så du kan inte bryta ut $x^{2}$ .

Använd tipset från jonis10 om att ersätta $x^{2}$ med t i ursprungsekvationen, dvs $t = x^{2}$

Då får du en vanlig andragradsekvation som du kan lösa lätt.

När du har gjort det så har du fått fram två rötter $t_{1}$ och $t_{2}$ .

Sedan löser du de båda ekvationerna $t_{1} = x^{2}$ och $t_{2} = x^{2}$ för att få fram alla fyra x-lösningar.

Det här var en besvärlig sak.

Läs tipsen du har fått en gång till.

Om du inte förstår så fråga gärna.

Nu förstår jag inte. Hur ska jag sätta t?

Du har ekvationen $x^4 - 8x^2 + 7 = 0$ . Om du byter ut $x^2$ mot $t$ får du ekvationen $t^2 - 8x + 7 = 0$ . Den ekvationen kan du lösa. Sedan fortsätter du som Yngve förklarade.

Om jag ger ett exempel $x^{4} + x^{2} + 5 = 0$ och jag säger att $x^{2} = t$

$x^{4} + x^{2} + 5 = 0 \Leftrightarrow x^{2} \cdot x^{2} + x^{2} + 5 = 0 t \cdot t + t + 5 = 0 \Leftrightarrow t^{2} + t + 5 = 0$

$x^{2} (x^{2} - 8 + 7) - - - - - - - t (t^{2} - 8 t + 7) = 0 m e n a r d u s å h ä r ?$

smaragdalena skrev :
Du har ekvationen $x^4 - 8x^2 + 7 = 0$ . Om du byter ut $x^2$ mot $t$ får du ekvationen $t^2 - 8x + 7 = 0$ . Den ekvationen kan du lösa. Sedan fortsätter du som Yngve förklarade.

Antar att du mena $t^{2} - 8 t + 7 = 0$

Ja,så menar jag.

Päivi skrev :
$x^{2} (x^{2} - 8 + 7) - - - - - - - t (t^{2} - 8 t + 7) = 0 m e n a r d u s å h ä r ?$

Fortfarande $x^{2} (x^{2} - 8 + 7) = x^{4} - 8 x^{2} + 7 x^{2}$ det är inte samma sak som din ursprungsekvation ser du det?

Nu förstår jag inte, hur jag ska göra.

Du har alltså att din ursprungliga ekvation är

$x^4 - 8x^2 + 7 = 0$

Sätter man nu $t = x^2$ så får man att

$t^2 - 8t + 7 = 0$

Detta är en andragradsekvation som du kan lösa.

Jag ursäktar om det blev lite otydlig men du skriver om fel sak flera gånger. Men som både Yngve och jag sa:

Du har ekvationen $x^{4} - 8 x^{2} + 7 = 0$ vi ersätter $x^{2} = t$ vi får då en andragradsfunktion

$t^{2} - 8 t + 7 = 0$ då kan du lösa vilka nollställen den ekvationen har. När du vet det sätter du

$t_{1} = x^{2} t_{2} = x^{2}$

Ekvationen är löst

Vad fick du för lösningar?

Päivi skrev :
Ekvationen är löst

Vad fick du för lösningar?

$t_{1} = 7 t_{2} = 7 t_{3 =} 1 t_{4} = 1$

Du har löst en andragradsekvation i t och den har två lösningar, nämligen $t_{1} = 7$ och att $t_{2} = 1$ .

Nu ska du hitta de värden på x som dessa lösningar motsvarar.

Kom ihåg att $x^{2} = t$ .

Om då t = 1 så blir x = ...?

Om då t = 7 så blir x = ...?

Noll

Nja nästan du vet att $t_{1} = 7 t_{2} = 1$ men vi sa att $x^{2} = t$ om vi ersätter $t_{1}$ och $t_{2}$ . Sedan löser du ut x så hittar vi dom sökta nollställen.

Päivi skrev :
Noll

Vad är det som är noll?

jonis10 skrev :
Nja nästan du vet att $t_{1} = 7 t_{2} = 1$ men vi sa att $x^{2} = t$ om vi ersätter $t_{1}$ och $t_{2}$ . Sedan löser du ut x så hittar vi dom sökta nollställen.

Nu förstår jag inte.

Päivi skrev :
jonis10 skrev :
Nja nästan du vet att $t_{1} = 7 t_{2} = 1$ men vi sa att $x^{2} = t$ om vi ersätter $t_{1}$ och $t_{2}$ . Sedan löser du ut x så hittar vi dom sökta nollställen.
Nu förstår jag inte.

Förstår du att din andragradsekvation $t^{2} - 8 t + 7 = 0$ har endast två lösningar, nämligen $t_{1} = 7$ och $t_{2} = 1$ ?

Ska jac ersätta de som nu heter t = 7 i andragrads ekvationen?

Päivi skrev :
Ska jac ersätta de som nu heter t = 7 i andragrads ekvationen?

Jag förstår inte vad du menar.

Du vet att $t = x^{2}$ , eller hur?

Om t nu är lika med 7, vad är då x?
Och om t är lika med 1, vad är då x?

Det ska vara roten ur av det som jag fick fram.

x = roten ur 7

Päivi skrev :
Det ska vara roten ur av det som jag fick fram.

Ja. Kan du skriva de två ekvationerna du ska lösa?

Och lösa dem? Vilka värden på x får du då?

Din andragradsekvation har två lösningar, t = 7 och t = 1. Detta motsvarar att $x^2 = 7$ respektive $x^2 = 1$ . Var och en av dessa andragradsekvationer har två lösningar. Sammanlagt blir det 4 olika lösningar till fjärdegradsekvationen.

Jag var tvungen titta, vad min sambo har förklarat till mig. Leta svar på saken,

Roten ur 7= 2,6

roten ur 1.= 1

t.= 7

t= -1

Päivi skrev :
Roten ur 7= 2,6
roten ur 1.= 1
t.= 7
t= -1

Andragradsekvationen x^2 = 7 har två lösningar. Vilka?

Andragradsekvationen x^2 = 1 har två lösningar. Vilka?

Tillsammans blir det fyra lösningar. Vilka?

Jag skulle vilja slänga min telefon. Den är jobbig.

Skriv på datorn då.

+ $t_{1} = \sqrt{7} = 2.6 t_{2} = \sqrt{1} = 1 t_{3} = 7 t_{4} = 1$

Päivi skrev :
+ $t_{1} = \sqrt{7} = 2.6 t_{2} = \sqrt{1} = 1 t_{3} = 7 t_{4} = 1$

Nej det stämmer inte.

Vi tar en ekvation i taget.

Vilka lösningar har ekvationen x^2 = 7?

49

x^2= 7

x= +- roten ut7

Päivi skrev :
x^2= 7
x= +- roten ut7

Ja!

Du har alltså två x-lösningar: $x_{1} = \sqrt{7}$ och $x_{2} = - \sqrt{7}$ .

Det finns ytterligare två x-lösningar, nämligen de man får om man löser ekvationen $x^{2} = 1$ . Vilka är det?

Jag somnade bort helt plötsligt.

Svarets -roten ur 1

Päivi skrev :
Jag somnade bort helt plötsligt.
Svarets -roten ur 1

Ja. Plusminus roten ur 1, dvs 1 och -1.

Nu har du fyra x-lösningar:

rotenur(7)
- rotenur(7)
1
-1

Då är det bara att kontrollera att alla dessa uppfyller ursprungsekvationen och sen är du klar.

Yngve!

När jag är riktigt sömnig, då vet jag inte vad jag än gör. Jag räknar fel. Det har hänt flera gånger för mig att jag sover bredvid matte bok.