Flerdim - partiell diffekvation

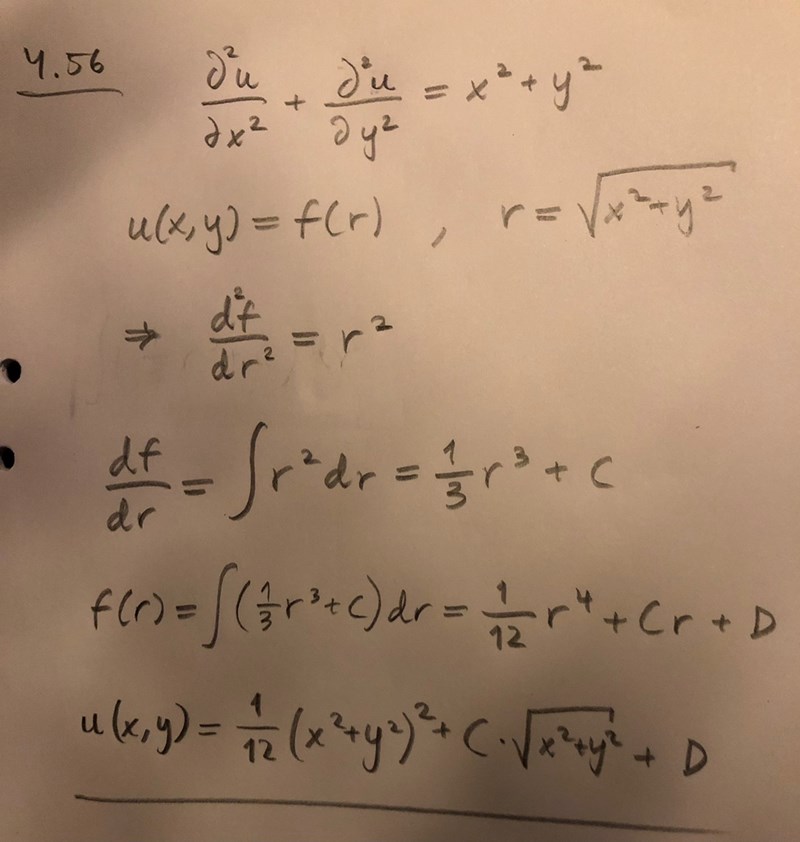Verkar som att jag har gjort en duktig tankevurpa här. Vad har jag gjort för fel?

EDIT: PDEs är nytt för mig så jag har egentligen lite problem att förstå uppgiften. Jag tolkar det som att funktionen med polära koordinater beror enbart på r, dvs alla vinklar ger ut samma funktionsvärde. Jag är dock inte helt övertygad om mitt eget resonemang.

Gäller det verkligen att $\frac{d^{2} f}{d r^{2}} = r^{2}$ bara för att $\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} = x^{2} + y^{2} (= r^{2})$ ? Jag är osäker på detta, men det var den enda lösningen jag kunde tänka mig.

Det blev ju tyvärr fel, men svaret i facit antyder att de har gjort ungefär likadant.

Hej,

Här har du samma uppgift redan diskuterad. Fråga om det är något du inte förstår.

$\Delta f = r^2$

$\frac{\partial^2 f}{\partial r^2}+\frac1r \frac{\partial f}{\partial r}=r^2$

Eftersom $\frac{\partial f}{\partial \theta}=0$

Tack. Min tankevurpa var att jag glömde att r är en funktion av x och y, så jag tog inte hänsyn till kedjeregeln. Sen var kedjeregeln också ganska klurig vid upprepning, men det blev lite tydligare efter det länkade inlägget, så jag kunde till slut komma fram till rätt svar.

Svara Avbryt

Visa senaste svar