Flervariabel-analys Greens Formel

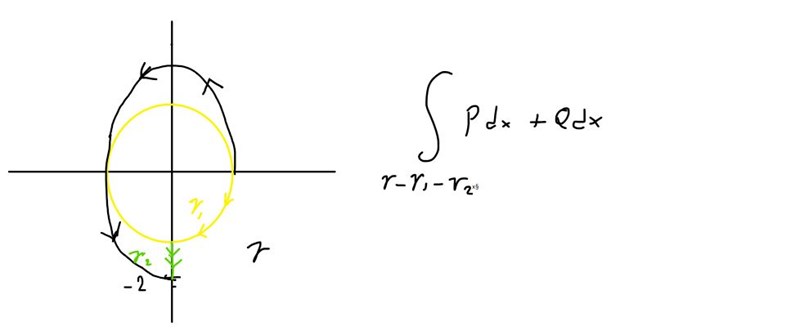
Hej,

Nej.

Du ska undvika att den positivt orienterade slutna kurvan omsluter singulära punkten (origo).

Albiki skrev:

Hej,

Nej.

Du ska undvika att den positivt orienterade slutna kurvan omsluter singulära punkten (origo).

aha så du menar att linjen γ2 är fel, hur kan man kompletera kurvan då?

Kan jag beräkna med hela enhetscirkeln och sedan ta bort pi/2

Alltså jag paramitiserar enhets cirkeln (cost,sint) , t:0->2pi 

En sluten positivt orienterad kurva som ej innesluter singulära punkten är

    $\partial D=\gamma \cup \gamma_1 \cup \gamma_2$

där $\gamma_1$ är rät linje som startar i punkten $(0,-2)$ och slutar i punkten $(0,-1)$ och $\gamma_2$ är trekvarts-cirkel som startar i punkten $(0,-1)$ och slutar i punkten $(1,0)$.

    $\displaystyle\oint_{\partial D}=\oint_\gamma + \oint_{\gamma_1}+\oint_{\gamma_2}$

och Greens formel kan tillämpas på $\partial D$ så $\oint_{\partial D} = \iint_D$ så att den sökta kurvintegralen blir

    $\displaystyle\oint_\gamma = \iint_D-\oint_{\gamma_1}-\oint_{\gamma_2}.$

• Parameterisering av $\gamma_1$:

        $\{(x,y):x=0 \text{ och } y=t \ , -2\leq t \leq -1\}$

ger motsvarande kurvintegral

    $\displaystyle\oint_{\gamma_1}P\,dx+Q\,dy = \int_{t=-2}^{-1} 0\,dt = 0$.

• Parameterisering av $\gamma_2$:

        $\{(x,y):x=\cos t \text{ och }y=\sin t \ , 0\leq t\leq \frac{3\pi}{2}\}$

ger motsvarande kurvintegral

    $\displaystyle\oint_{\gamma_2}P\,dx+Q\,dy=\int_{t=\frac{3\pi}{2}}^{0}dt = -\frac{3\pi}{2}$.

Albiki skrev:

• Parameterisering av $\gamma_1$:

        $\{(x,y):x=0 \text{ och } y=t \ , -2\leq t \leq -1\}$

ger motsvarande kurvintegral

    $\displaystyle\oint_{\gamma_1}P\,dx+Q\,dy = \int_{t=-2}^{-1} 0\,dt = 0$.

• Parameterisering av $\gamma_2$:

        $\{(x,y):x=\cos t \text{ och }y=\sin t \ , 0\leq t\leq \frac{3\pi}{2}\}$

ger motsvarande kurvintegral

    $\displaystyle\oint_{\gamma_2}P\,dx+Q\,dy=\int_{t=\frac{3\pi}{2}}^{0}dt = -\frac{3\pi}{2}$.

Vi får samma svar 3pi/2. Så det går att räkna med en hel ellips och cirkel och sedan ta bort 1/4 

BabySoda skrev:

Visa spoiler

Albiki skrev:

• Parameterisering av $\gamma_1$:

        $\{(x,y):x=0 \text{ och } y=t \ , -2\leq t \leq -1\}$

ger motsvarande kurvintegral

    $\displaystyle\oint_{\gamma_1}P\,dx+Q\,dy = \int_{t=-2}^{-1} 0\,dt = 0$.

• Parameterisering av $\gamma_2$:

        $\{(x,y):x=\cos t \text{ och }y=\sin t \ , 0\leq t\leq \frac{3\pi}{2}\}$

ger motsvarande kurvintegral

    $\displaystyle\oint_{\gamma_2}P\,dx+Q\,dy=\int_{t=\frac{3\pi}{2}}^{0}dt = -\frac{3\pi}{2}$.

 

Vi får samma svar 3pi/2. Så det går att räkna med en hel ellips och cirkel och sedan ta bort 1/4 

Nej.

Du verkar ha missförstått varför jag konstruerade kurvan $\partial D$ som jag gjorde. Läs Greens formel noggrant och fäst särskild uppmärksamhet vid satsens förutsättningar. Ta sedan en ordentligt titt på det aktuella vektorfältet.

Albiki skrev:

BabySoda skrev:

Visa föregående citat

Visa spoiler

Albiki skrev:

• Parameterisering av $\gamma_1$:

        $\{(x,y):x=0 \text{ och } y=t \ , -2\leq t \leq -1\}$

ger motsvarande kurvintegral

    $\displaystyle\oint_{\gamma_1}P\,dx+Q\,dy = \int_{t=-2}^{-1} 0\,dt = 0$.

• Parameterisering av $\gamma_2$:

        $\{(x,y):x=\cos t \text{ och }y=\sin t \ , 0\leq t\leq \frac{3\pi}{2}\}$

ger motsvarande kurvintegral

    $\displaystyle\oint_{\gamma_2}P\,dx+Q\,dy=\int_{t=\frac{3\pi}{2}}^{0}dt = -\frac{3\pi}{2}$.

 

Vi får samma svar 3pi/2. Så det går att räkna med en hel ellips och cirkel och sedan ta bort 1/4 

Nej.

Du verkar ha missförstått varför jag konstruerade kurvan $\partial D$ som jag gjorde. Läs Greens formel noggrant och fäst särskild uppmärksamhet vid satsens förutsättningar. Ta sedan en ordentligt titt på det aktuella vektorfältet.

Du konstruerade ∂D väll för att komplettera ellips kurvan, alltså felet jag gjorde från första början är att jag tog fel håll på cirkeln och linjen. Hade jag vänt på de så hade jag fått rätt svar.