Flervariabel, volymen under ytan och maximum värdet
Tja!
Jag har fastnat på de två uppgifterna nedan.
Båda uppgifterna tillhör samma frågeställning och information.
Jag fattar inte riktigt hur jag ens ska börja.


Jag uppskattar verkligen all hjälp.
Börja med att rita upp området. Vilka värden kan f(x,y) ha på området?
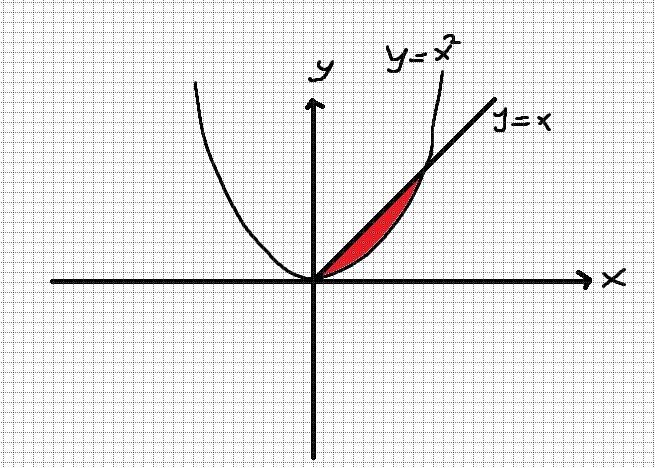
Jag ritade bilden nedan.
Det röda området mellan linjerna är området i D.
Bilden i område S beror väl på, där C kan väljas. Det blir en hyperbel.
Funktionsytan S är entydigt bestämd. Vilka värden kan z = f(x,y) anta på området D?
Jag har ingen aning.
Om jag skulle gissa tror jag allting över området D i första kvadranten, alltså då x>0 och y>0.
Om vi börjar med origo (det ingår ju i D). Vilket z-värde har punkten? Du vet ju att z = f(x,y) och att f(x,y) = x2-y2.
Ok, som du sa ingår origo, då borde x=0 och y = 0
vilket ger : z = f(0,0) = 0.
Om vi följer den räta linjen y = x från (0,0) till (1,1), hur kommer z att variera längs denna linje?
Om vi följer parabeln y = x2 från (0,0) till (1,1), hur kommer z att variera längs denna kurva?
z kommer hela tiden att vara 0.
Efter att ha hittat funktionens största värde på randen av D så fortsätter du med att hitta eventuella stationära punkter av f i D. Jämför dessa och se vilken som är störst.
Har du även problem med 1D?
På den räta linjen, ja, men inte på parabeln.
Ja, jag har också problem med 1D.
Jag förstår faktiskt inte hur z kommer variera längs parabeln.
Du vet att koordinaterna för alla punkter på kurvan är (x,x2). Du skall alltså beräkna z = x2-y2 som in det här fallet blir z=x2-x4. Vilket är det största och minsta värdet z har på parabeln?
Jag antar att det största värdet blir z = 1 och det minsta z= 0
om man skriver om uttrycket:
men x >0 så x = -1 förkastas.
ogrelito skrev:Jag antar att det största värdet blir z = 1 och det minsta z= 0
om man skriver om uttrycket:
men x >0 så x = -1 förkastas.
Hur får du z att bli 1?
Jag får
För vilket värde på parabeln får du att z = 1? Jag hittar inget värde som är så stort.
Ignorera det jag skrev innan. Jag gissade bara.
Jag beräknade ett nytt värde.
Jag fick ett max z = och ett min z = 0
Jag vet inte om det är rätt men jag gjorde såhär:
Det kan vara bra att ta reda på om funktionen z =x2-y2 har några extrempunkter på sitt inre också, som Qetsiyah tipsade om tidigare. Vet du hur du skall ta reda på detta?
Jag tror det. Menar du att jag ska ta dubbel derivatan och sedan använda hess matrisen för att ta reda på om vi har någon max, min eller sadelpunkt för våra kritiska punkter, då ()?
I svaret står det att jag ska komma fram till 1/70. Vad gör jag efter att jag har hittat en sadelpunkt i D och en max och min punkt på randen D. Skulle någon också kunna hjälpa mig med 1 E)
När blir funktionsvärdet vilket är svaret på uppgift 1D. Punkten (0,0) ingår inte i D.
För 1E ska du beräkna integralen
Juste då fattar jag!
Tack så mycket för hjälpen!





