Flöde flervarre
Någonstans tänker jag antagligen helt fel, men jag fattar inte. Har nog inte riktigt greppat detta kapitlet i boken.
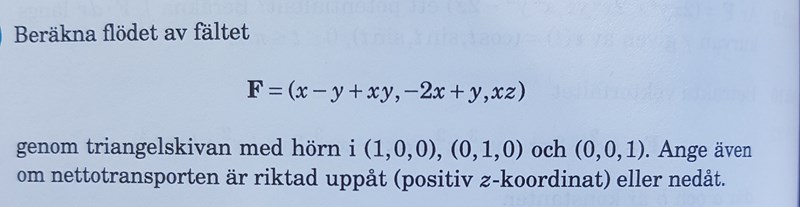

Svaret är 1/12 nedåt
Har jag tänkt rätt nu? 🤷♀️ (svaret blir iaf rätt)
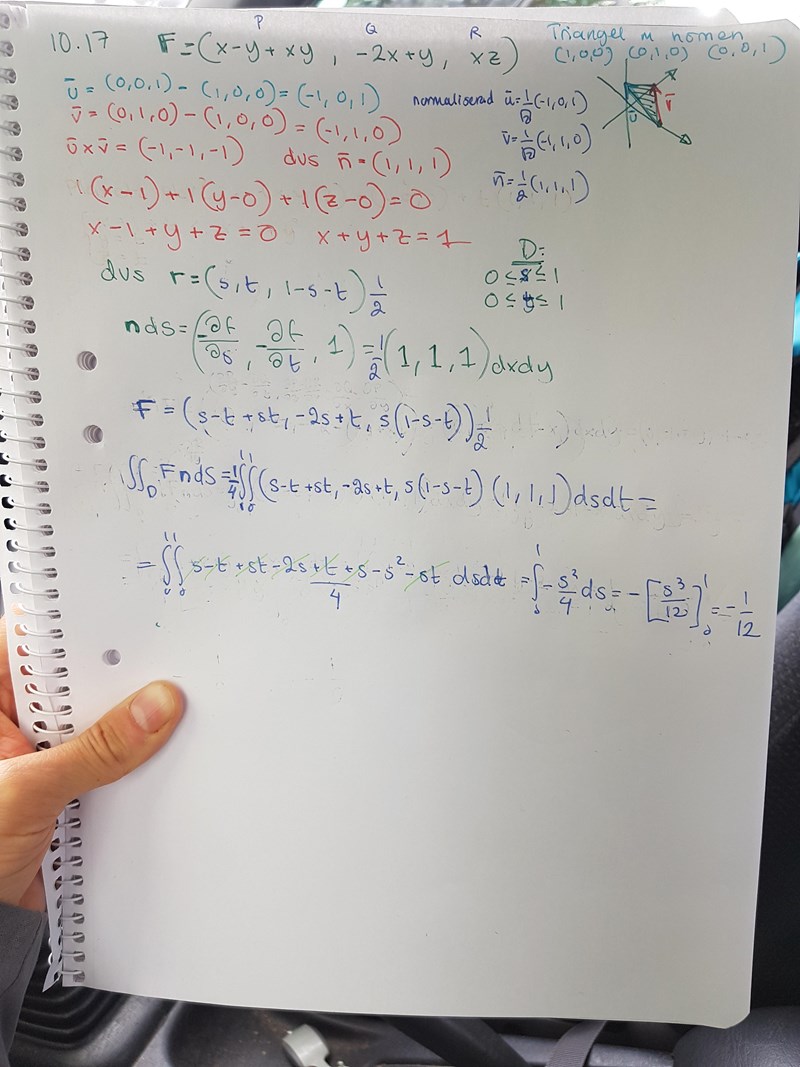
Varför dyker det upp en faktor här?
Jag tycker att du ska parametrisera den gröna triangelytan över den bruna triangelformade bottenytan D (se bild nedan) så här
Ett annat, kanske enklare, alternativ är följande: I ovanstående figur har (enkel kalkyl) det grönrutiga planet, kallat S, ekvationen x+y+z-1=0, vilken är en nivåyta G(x,y,z)=0. Härav: Ytelementet , enhetsnormalen utåtriktad.
, där R är det bruna triangelområdet i ovanstående figur. Med insatta gränser i dubbelintegralen , landar vi i det uttryck du själv räknat fram.
Jroth skrev:Varför dyker det upp en faktor här?
Jag tycker att du ska parametrisera den gröna triangelytan över den bruna triangelformade bottenytan D (se bild nedan) så här
Jag improviserade och typ normaliserade allt 🙈. Deaperat försök. Jag har provat räkna om igen, men jag fattar inte hur jag ska tänka när det gäller definitionsmängden D. Jag halkar helatiden tillbaka till att både s och t går mellan 0 och 1 trots att jag fattar att det inte borde vara så. Anledningen att jag tänker så är att om s representerar x och x går mellan 0 och 1 borde även s göra det och på motsv sätt med t.
Har du möjliget att förklara?
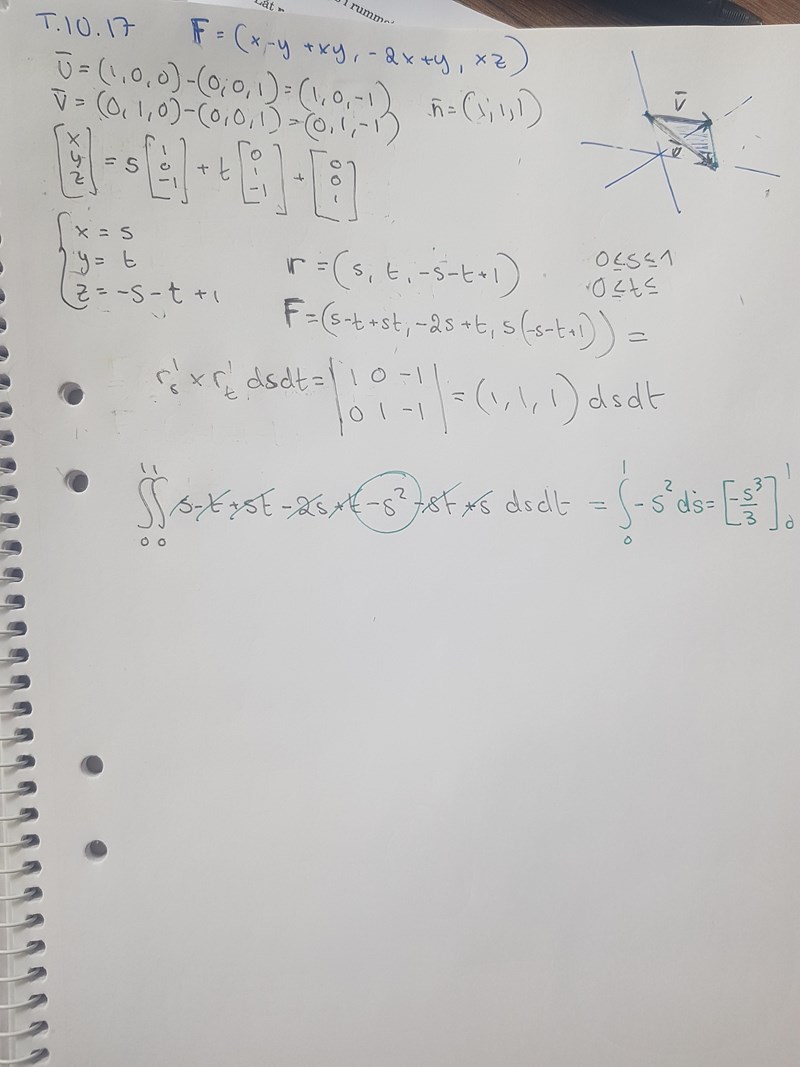
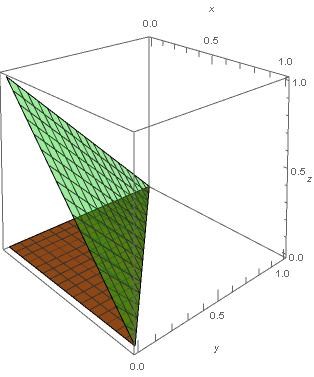
Om vi tittar på den bruna bottenytan från ovan ser den ut så här (den ligger i xy-planet)
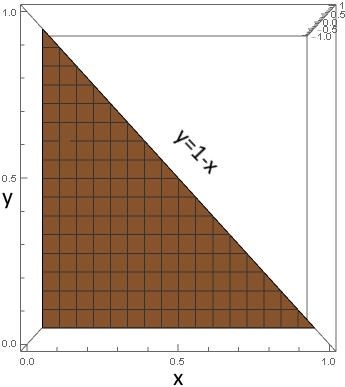 Vi ser att för varje värde på får variera från upp till linjen .
Vi ser att för varje värde på får variera från upp till linjen .
Med din parametrisering (där ) ska gränserna för det bruna området vara
Integralen blir alltså
Jroth skrev:Om vi tittar på den bruna bottenytan från ovan ser den ut så här (den ligger i xy-planet)
Vi ser att för varje värde på får variera från upp till linjen .
Med din parametrisering (där ) ska gränserna för det bruna området vara
Integralen blir alltså
Tack för förklaringen! Jag måste öva mer för att fatta helt. När du illustrerar, men så fort det blir en ny situation har jag svårt att applicera samma metod. Det räcker med att ytan blir en kvadrat ryp 🤦♀️. Nu får jag ett negativt svar, om jag förstår det rätt betyder det att flödet går på andra hållet. Tänker jag rätt då?
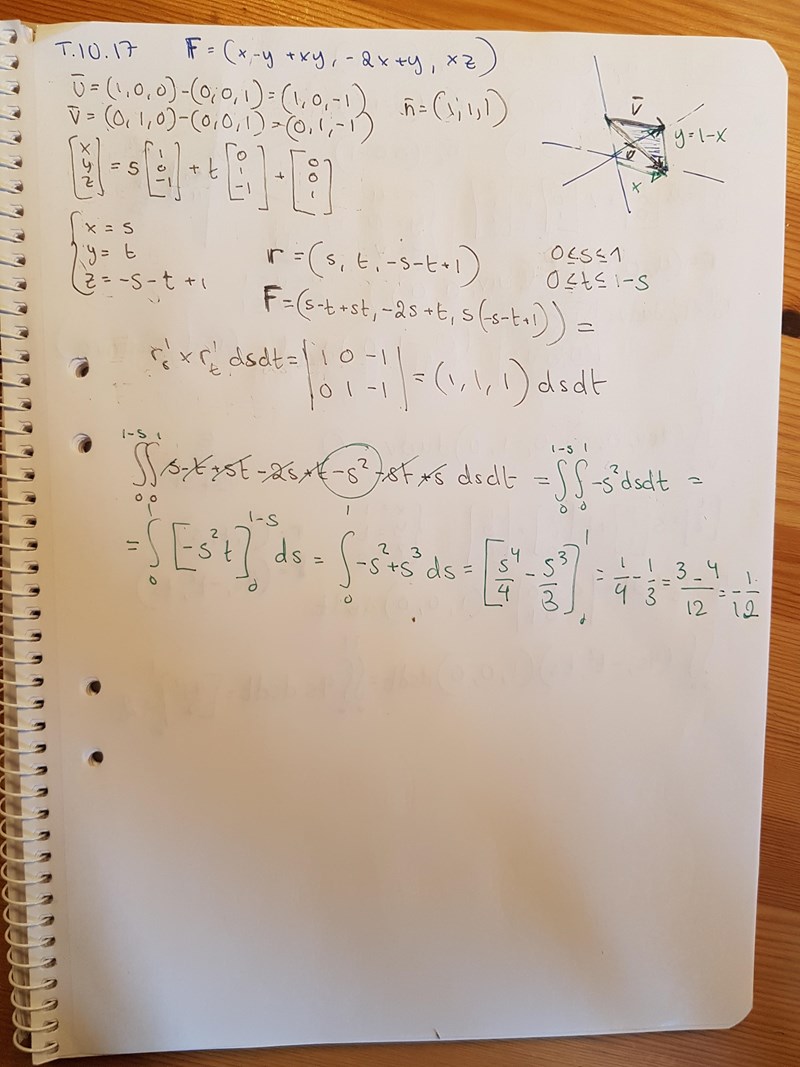
Ja, du har beräknat flödet genom ytan med och får ett negativt svar. Det innebär att flödet går åt "andra hållet", alltså ned mot den bruna ytan.
är vektor med riktning (vilket naturligtvis är samma som en normal till planet). Eftersom den har positiv z-komponent pekar den "snett" uppåt.
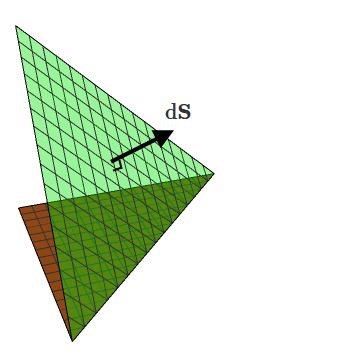
Att du får ett negativt värde innebär att flödet går ner mot den bruna ytan (i motsatt riktning)



