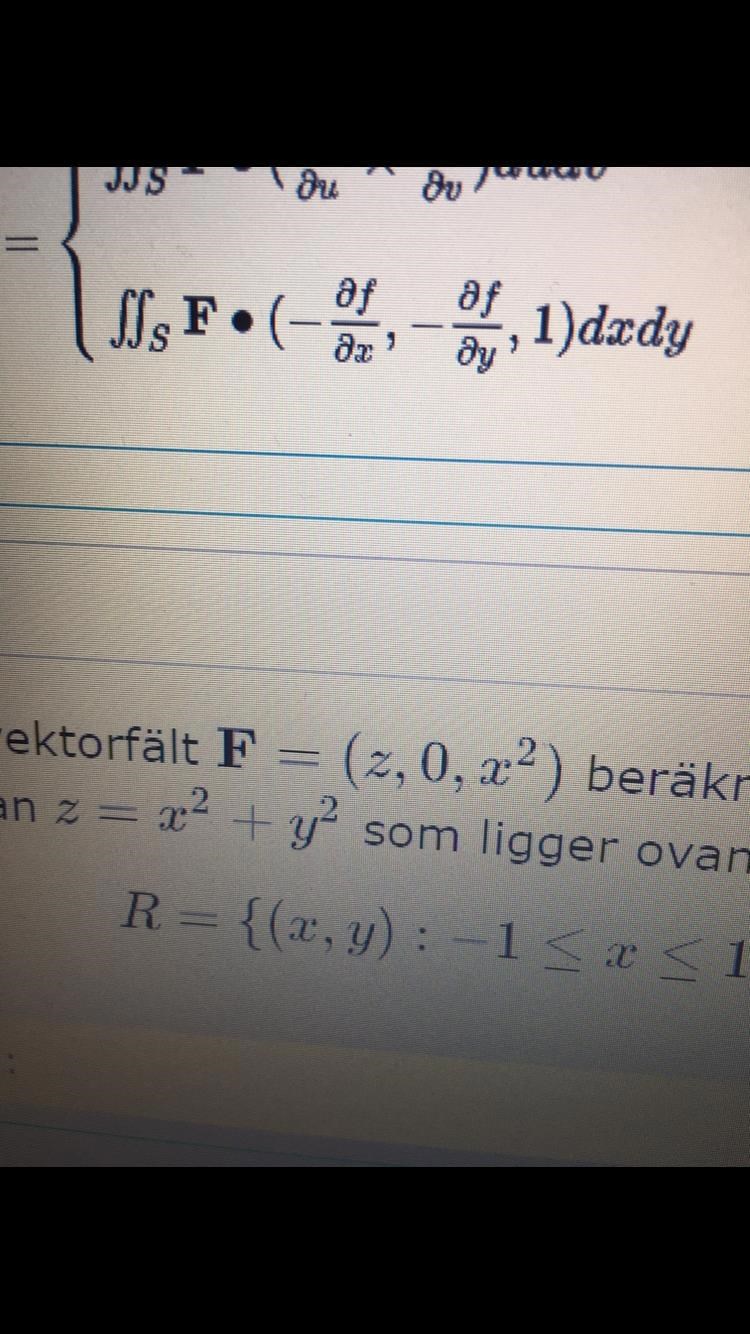Flödesintegralens definition
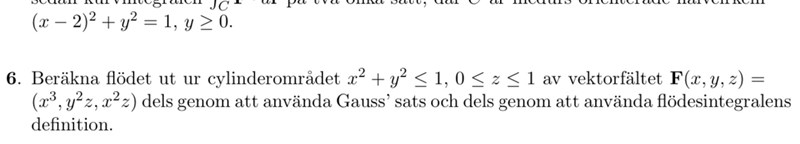
 Hej, i uppgiften behöver Vi beräkna flödet med hjälp av flödesintegralensdefinition.
Hej, i uppgiften behöver Vi beräkna flödet med hjälp av flödesintegralensdefinition.
men i lösningen, delar vi området I tre delytor.
Och mitt fråga är att värför delar vi området I tre delytor. Och värför är normalen till s2 är lik (0,0,-1) och inte samma som normalen till s1. Och hur beräknar vi den normalen till s3.
delar vi området för att orientering på ytan ska vara positiv.
Normalen till locket pekar åt motsatt håll jämfört med
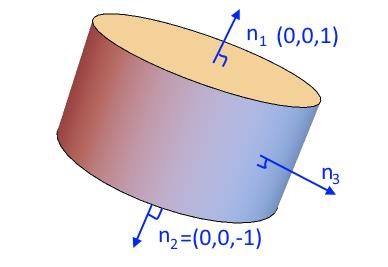 Normalen pekar ut från mantelytan i radiell led . Normalen till mantelytan pekar alltså hela tiden ut från cylindern och är vinkelrät mot ytan. Det betyder att den har olika riktning beroende var på ytan du är.
Normalen pekar ut från mantelytan i radiell led . Normalen till mantelytan pekar alltså hela tiden ut från cylindern och är vinkelrät mot ytan. Det betyder att den har olika riktning beroende var på ytan du är.
För att räkna ut normalen kan du parametrisera mantelytan i en vinkel och en z-koordinat.
Då blir normalen
Ett lite enklare sätt är att inse att den alltid pekar i radiell led , vilket innebär
I just det här fallet är varför
Hej, och tack för din svar, jag vet inte hur i lösningen beräknas normalen n3, eftersom om vi ser på området som grafen på en funktion f(x,y)=(x^2+y^2). Och använder formelen i bilden, så får jag N=(-2x,-2y,1) och inte (x,y,0). Så hur beräknar vi denna normalen
Du kan inte använda standardparametriseringen för mantelytan.
Mantelytan kan du parametrisera i cylinderkoordinater
För mantelytan gäller att , . En parameterframställning för mantelytan är därför
där och .
Vilket är samma sak som (x,y,0) då .
hej, tack så mycket, så du menar att eftersom radien för cirkelen är lika med ett, är x=1*cos(φ), och y=1*sin(φ)
suad skrev:hej, tack så mycket, så du menar att eftersom radien för cirkelen är lika med ett, är x=1*cos(φ), och y=1*sin(φ)
Ja, just det.
tack så mycket, det var till stor hjälp