Flödet av B ur klotet r=R
Hej!
Jag fick teckenfel på uppgiften. Vad beror det på? Facit fick ett positivt tecken, förstår inte varför.
Varför integrerar du inte över sfären r = R direkt? Blir det inte att gå över ån efter vatten att införa också integration över en annan sfär med en annan radie?
Vilken normal har du på sfären r = R? Vilken normal har du på sfären r = epsilon?
PATENTERAMERA skrev:Varför integrerar du inte över sfären r = R direkt? Blir det inte att gå över ån efter vatten att införa också integration över en annan sfär med en annan radie?
Vilken normal har du på sfären r = R? Vilken normal har du på sfären r = epsilon?
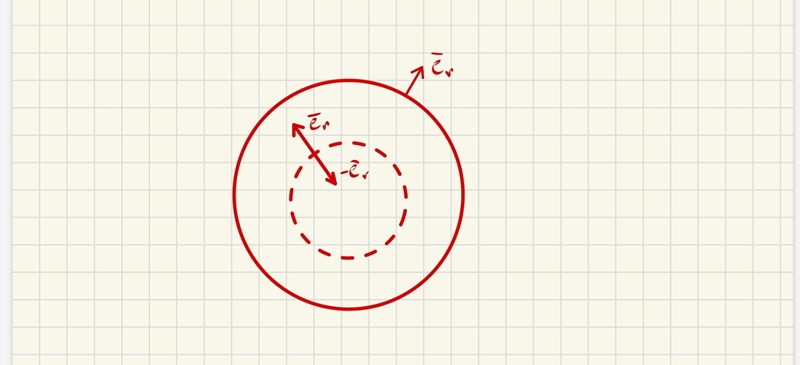
Det går inte att göra det pga origo är inte definierad för fältet. Därför införde jag en liten sfär med r=epsilon. Det är väl den metoden som gäller? Normalen på stora sfären r =R är väl er och normalen på lilla sfären är väl er också,men det ska dock vara -er och jag vet inte varför.
Nja, du tänker på om du skulle använda Gauss sats. Det behövs inte här; fältet är är ju väldefinierat överallt på sfären r = R, så det är bara att integrera.
Eftersom divB = 0 så kan du med Gauss visa att flödet ut från sfären r = R plus flödet in i sfären r = epsilon är lika med noll. Eller ekvivalent, flödet ut ur sfären r = epsilon är lika med flödet ut ur sfären r = R. Det är därför du får teckenfel.
PATENTERAMERA skrev:Nja, du tänker på om du skulle använda Gauss sats. Det behövs inte här; fältet är är ju väldefinierat överallt på sfären r = R, så det är bara att integrera.
Eftersom divB = 0 så kan du med Gauss visa att flödet ut från sfären r = R plus flödet in i sfären r = epsilon är lika med noll. Eller ekvivalent, flödet ut ur sfären r = epsilon är lika med flödet ut ur sfären r = R. Det är därför du får teckenfel.
Jag förstår inte hur du menar att man kan integrera här när 0 inte är definierad för fältet. Ja jag valde gaus sats för det var lättare att komma på det. Teckenfel beror nog på det här med normalriktning på lilla sfären. Egentligen ska e_r på lilla sfären var inåtriktad om ytan mellan r=epsilon och r=R anger volymen mellan dem
När du använder Gauss så använder du att flödet ut ur ett slutet område är lika med volymsintegralen av divergensen. Här kan man se området som området mellan sfärerna. Så ut ur området betyder ut ur sfären r = R men in genom sfären r = epsilon. Eftersom divergensen är noll i hela området så följer det att flödet ut ur sfären r = R är lika med flödet ut ur sfären r = epsilon.
Du integrerar ju bara över sfären, och bara värden på sfären spelar roll. Vad fältet har eller inte har för värde i origo är inte relevant.
PATENTERAMERA skrev:När du använder Gauss så använder du att flödet ut ur ett slutet område är lika med volymsintegralen av divergensen. Här kan man se området som området mellan sfärerna. Så ut ur området betyder ut ur sfären r = R men in genom sfären r = epsilon. Eftersom divergensen är noll i hela området så följer det att flödet ut ur sfären r = R är lika med flödet ut ur sfären r = epsilon.
Du integrerar ju bara över sfären, och bara värden på sfären spelar roll. Vad fältet har eller inte har för värde i origo är inte relevant.
Jag förstår inte hur den beräkningen skulle se ut. Jag har som sagt inte gjort på det sättet utan gick över till gaus och rättade till tecknet.
