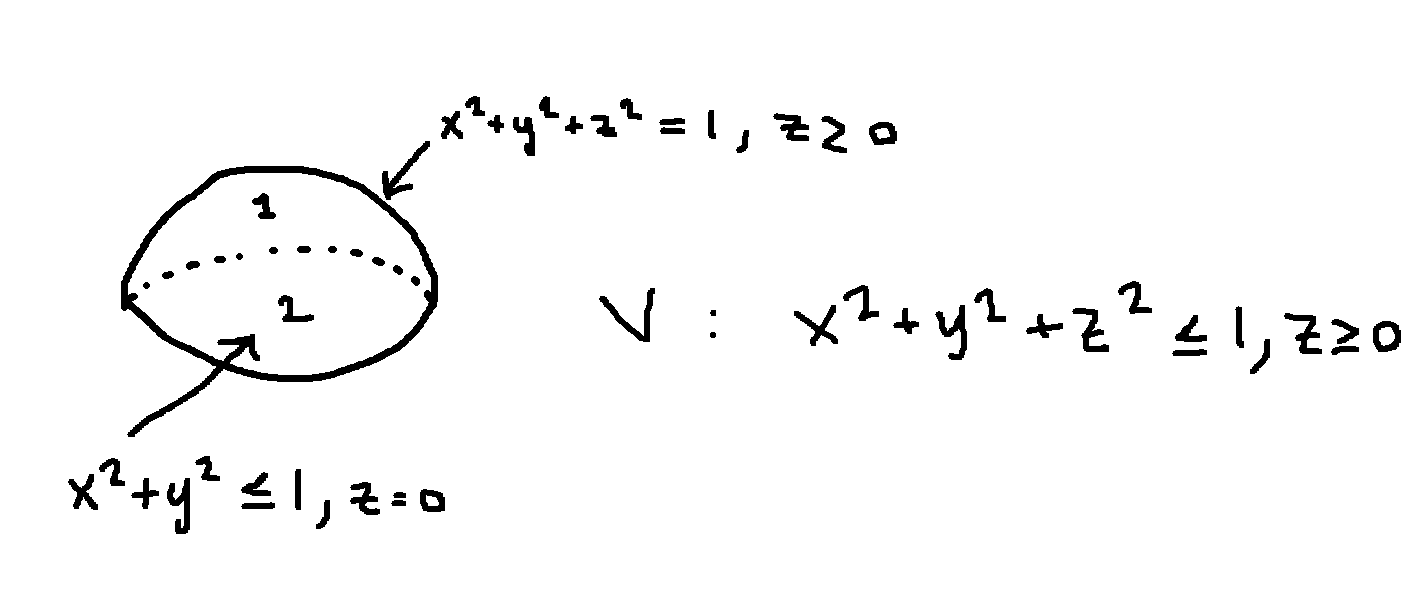Flödet genom vektorfältet


Hej!
Jag är lite fast med hur man hittar N (enhetsnormalen) och gränserna är jag osäker för både phi och theta. En av dem borde vandra mellan 0 till pi/2 och 0 till 2pi,men jag vet inte om det är vinkeln phi eller theta. Jag vet inte om det är lättare att använda divergenssatsen eller ytintegral ? För divergenssats så måste ytan vara sluten vilket jag utläser som att det inte är det.
Funkar inte gauss sats på liknande sett som greens sats? Du kanske kan utöka området till att vara halvklotet x^2 + y^2 + z^2 <= 1 och sedan subtrahera bort flödet genom det du har lagt till.
Lasse Vegas skrev:Funkar inte gauss sats på liknande sett som greens sats? Du kanske kan utöka området till att vara halvklotet x^2 + y^2 + z^2 <= 1 och sedan subtrahera bort flödet genom det du har lagt till.
Nu hänger jag inte med här riktigt. Andra halvsfären är väl hela klotet men hur ser den ekvationen ut ? Vad menar du med subtrahera och lägga till?
Man behöver inte utöka det med en halfsvär utan kan göra en sluten yta genom att lägga till en cirkelskiva på botten.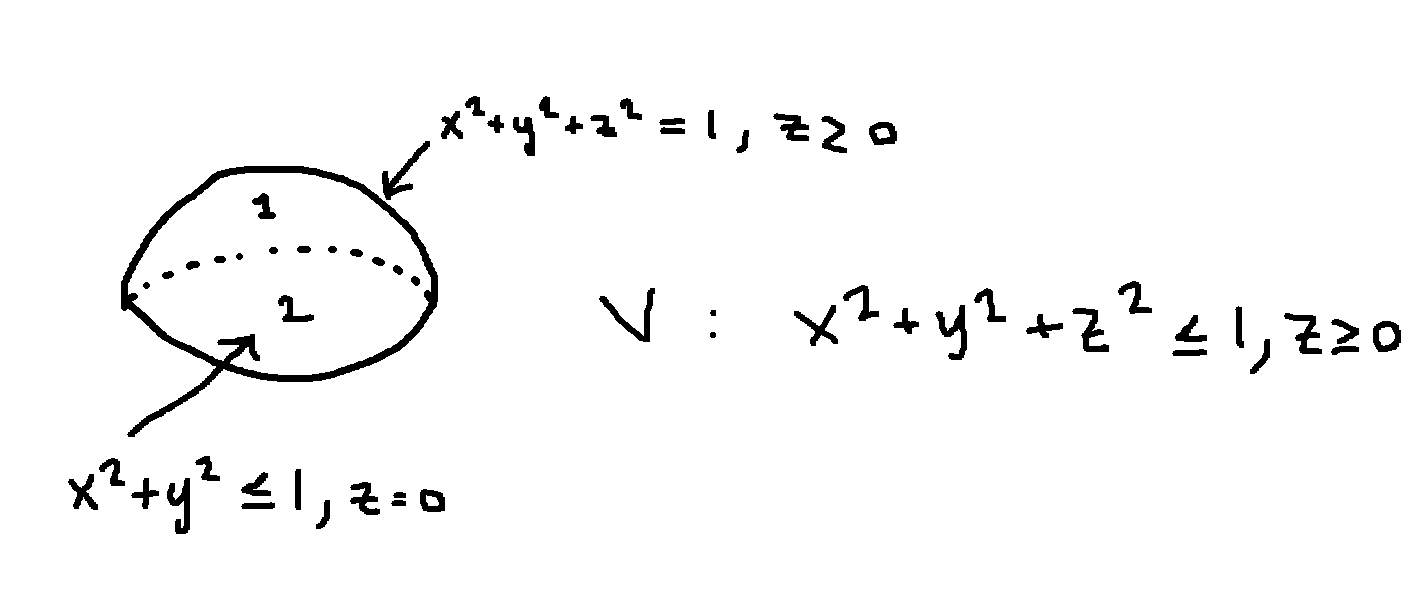 Nedre ytans enhetsnormal är ju dessutom bara .
Nedre ytans enhetsnormal är ju dessutom bara .
Lasse Vegas skrev:Man behöver inte utöka det med en halfsvär utan kan göra en sluten yta genom att lägga till en cirkelskiva på botten.
Men den där cirkelskiva på botten, är den inte en del av halvsfären? Jag trodde man skulle skapa en hel sfär för att liksom göra hela området slutet.
Det finns oändligt många sätt att göra ett område slutet, man kan t.ex utöka det till en hel sfär, men då behöver du ta bort det du har lagt till, dvs flödet genom nedre halvsfären. Och beräkningen för den nedre halvsfären blir ju liksom samma som för den övre halvsfären, så då måste man beräkna det i alla fall.
Lasse Vegas skrev:Det finns oändligt många sätt att göra ett område slutet, man kan t.ex utöka det till en hel sfär, men då behöver du ta bort det du har lagt till, dvs flödet genom nedre halvsfären. Och beräkningen för den nedre halvsfären blir ju liksom samma som för den övre halvsfären, så då måste man beräkna det i alla fall.
Jag förstår. Jag vill gärna utöka det till en helsfär isåfall. Hur gör jag då? Vad menar du med att man ska ta bort det man lagt till?
Vi ska bestämma flödet genom övre halvsfären. Utökar vi området till en helsfär så beräknar vi flödet genom hela sfären. Att beräkna flödet genom hela sfären kommer inte ge samma resultat som om vi enbart beräknade flödet genom halvsfären. För att motverka det problemet måste vi subtrahera flödet genom halvsfären vi lagt till för att det vi beräknar ska bli rätt.
Det är samma sak som för greens sats. Man kan utöka ett område och göra det slutet så att man kan använda greens sats, men när man utökar så ändrar man värdet som beräknas. Då måste man subtrahera kurvintegralen över den väg man lagt till för att inte ändra värdet.
Lasse Vegas skrev:Vi ska bestämma flödet genom övre halvsfären. Utökar vi området till en helsfär så beräknar vi flödet genom hela sfären. Att beräkna flödet genom hela sfären kommer inte ge samma resultat som om vi enbart beräknade flödet genom halvsfären. För att motverka det problemet måste vi subtrahera flödet genom halvsfären vi lagt till för att det vi beräknar ska bli rätt.
Det är samma sak som för greens sats. Man kan utöka ett område och göra det slutet så att man kan använda greens sats, men när man utökar så ändrar man värdet som beräknas. Då måste man subtrahera kurvintegralen över den väg man lagt till för att inte ändra värdet.
Ok då förstår jag. Så totala flödet (helsfär) = flöde över övre halvsfär+flöde övre nedre halvsfär , för att beräkna flöde över övre halvsfär som uppgiften frågar oss om så tar vi totala flöde -flöde över nedre halvsfär=flöde över övre halvsfär right?
Ok så hur beräknar man totala flöde då? Jag antar att vi har då en helsfär som ges som x^2+y^2+z^2<=1 ?
Det är för totala flödet som du kan använda gauss sats, och ja området blir då klotet x^2 + y^2 + z^2 <= 1.
Men som jag sa innan, det hjälper inte direkt att utöka området till en helsfär för att du behöver fortfarande beräkna flödet genom en halvsfär, vilket var anledningen till att vi använde gauss sats från första början.
Lasse Vegas skrev:Men som jag sa innan, det hjälper inte direkt att utöka området till en helsfär för att du behöver fortfarande beräkna flödet genom en halvsfär, vilket var anledningen till att vi använde gauss sats från första början.
Ja precis vi ska ju dra bort nedre halvsfären på slutet? Jag förstod det som att vi ska göra detta sist. Nu är fokuset att använda gaus sats för en helsfär och utför beräkningarna.
Lasse Vegas skrev:Det är för totala flödet som du kan använda gauss sats, och ja området blir då klotet x^2 + y^2 + z^2 <= 1.
Yes!
Flöde genom övre halvsfär = Flöde genom hela ytan - flöde genom nedre halvsfär.
Vi ville ju beräkna flödet genom övre halvsfären. Om vi utökar till en helsfär så ser vi att vi fortfarande måste bestämma flödet genom den nedre halvsfären, vilket är samma typ av beräkning som för den övre halvsfären. Det enda vi har gjort då är att lägga till en beräkning för totala flödet. Det blir alltså bara mer jobb. Men om vi istället utökar det med en cirkelskiva så får vi
Flöde genom övre halvsfär = flöde genom hela ytan - flöde genom cirkelskiva. Att beräkna flödet genom cirkelskivan är enklare och flödet genom hela ytan kommer att förbli ganska oförändrat.
Lasse Vegas skrev:Flöde genom övre halvsfär = Flöde genom hela ytan - flöde genom nedre halvsfär.
Vi ville ju beräkna flödet genom övre halvsfären. Om vi utökar till en helsfär så ser vi att vi fortfarande måste bestämma flödet genom den nedre halvsfären, vilket är samma typ av beräkning som för den övre halvsfären. Det enda vi har gjort då är att lägga till en beräkning för totala flödet. Det blir alltså bara mer jobb. Men om vi istället utökar det med en cirkelskiva så får vi
Flöde genom övre halvsfär = flöde genom hela ytan - flöde genom cirkelskiva. Att beräkna flödet genom cirkelskivan är enklare och flödet genom hela ytan kommer att förbli ganska oförändrat.
den där cirkelskivan förstår jag fortfarande inte var den kommer ifrån eller hur den är en del av en hela sfären ( får inte upp en bild i mitt huvud). Men vad synd att metoden med helsfär gör bara det jobbigare med beräkningar. Sen tror jag inte att jag ser hur det blir jobbigt med beräkningar för det makeade mer sense när vi pratade om det. Totala flöde genom helsfär-flöde genom nedre sfär=flöde genom övre halvsfär.
Tänk dig att vi har en sfär. En sfär är ihålig så om vi skär den i mitten får vi två halvsfärer (tänk dig att de ser ut som skålar), för att göra en halvsfär sluten kan vi sätta dit en cirkelskiva där vi delade sfären (tänk dig att vi sätter en platt tallrik på skålen). Då har vi en sluten yta som består av en halvsfär (skål) + en cirkelskiva (tallrik).
Lasse Vegas skrev:Tänk dig att vi har en sfär. En sfär är ihålig så om vi skär den i mitten får vi två halvsfärer (tänk dig att de ser ut som skålar), för att göra en halvsfär sluten kan vi sätta dit en cirkelskiva där vi delade sfären (tänk dig att vi sätter en platt tallrik på skålen). Då har vi en sluten yta som består av en halvsfär (skål) + en cirkelskiva (tallrik).
Vill du visa med en figur kanske? Så jag förstår var cirkelskivan kommer ifrån.
Här har vi en halvsfär och här har vi en cirkelskiva
och här har vi en cirkelskiva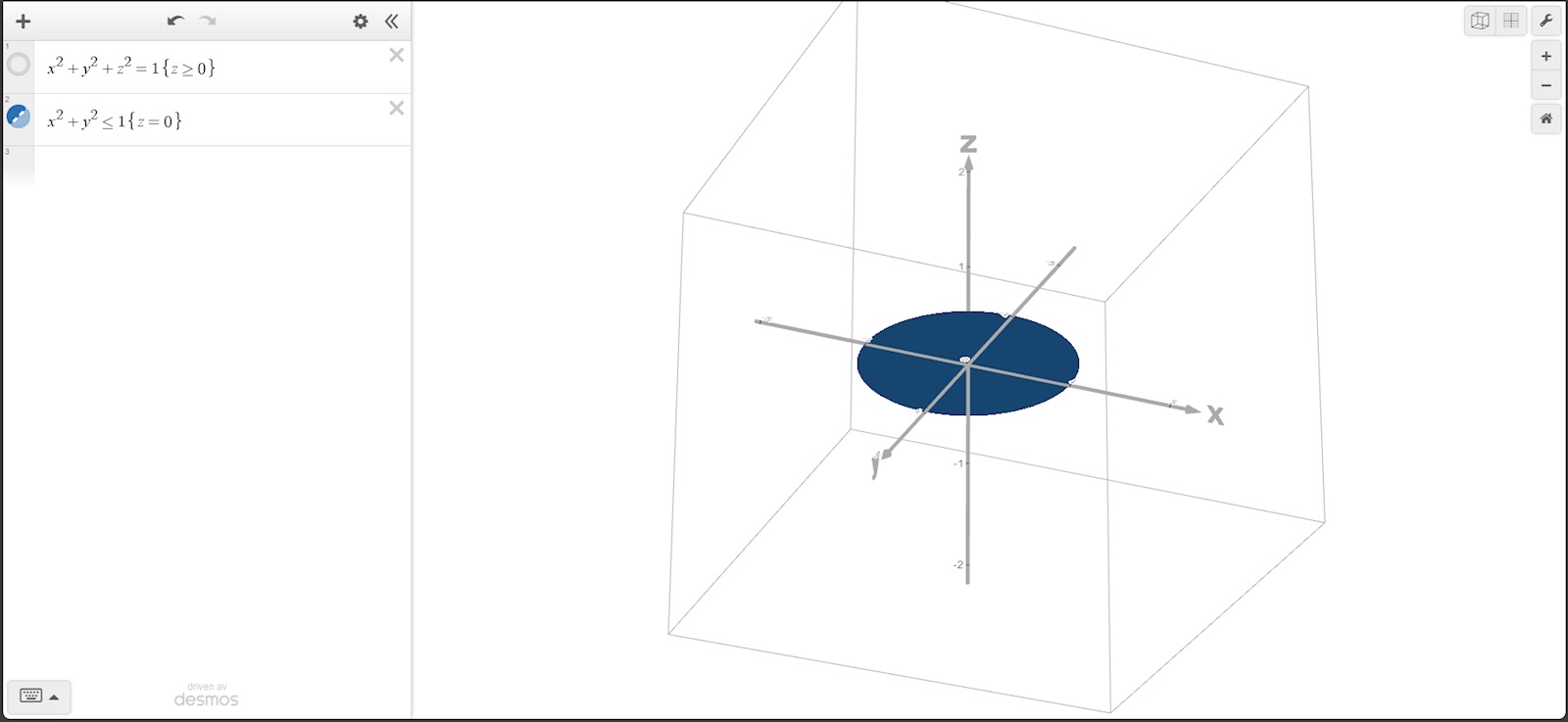 Utökar vi halvsfären med cirkelskivan får vi
Utökar vi halvsfären med cirkelskivan får vi  Du ser att cirkelskivan täcker till den öppna delen längst ner på halvsfären
Du ser att cirkelskivan täcker till den öppna delen längst ner på halvsfären
En sak jag tänkte på nu när jag läste frågan igen var att det står att man ska bestämma flödet "upp genom halvsfären". Det är lite dåligt formulerat men de kanske vill att man ska beräkna flödet genom ytan fast i z-riktningen (om vi forutsätter att z-axeln är riktad "upp").
Lasse Vegas skrev:En sak jag tänkte på nu när jag läste frågan igen var att det står att man ska bestämma flödet "upp genom halvsfären". Det är lite dåligt formulerat men de kanske vill att man ska beräkna flödet genom ytan fast i z-riktningen (om vi forutsätter att z-axeln är riktad "upp").
Vad menar man då? Är det gaus fortfarande som gäller eller inte? Området är inte slutet i alla fall.
Då kanske det är mer passande att beräkna det som vanligt. Jag minns dock inte hur man beräknar flödet i en speciell riktning, är det inte bara att byta ut ytnormalen mot den riktning man vill ha?
Lasse Vegas skrev:Här har vi en halvsfär
och här har vi en cirkelskiva
Utökar vi halvsfären med cirkelskivan får vi
Du ser att cirkelskivan täcker till den öppna delen längst ner på halvsfären
Okej, men vilken är den öppna delen på halvsfären? Jag tänker på den röda bilden som beskriver en halvsfär.
Lasse Vegas skrev:Då kanske det är mer passande att beräkna det som vanligt.
Hur då vanligt? Facit använde divergenssatsen. De var inne på det här med cirkelskiva och sånt som du nämnde om.
Med vanligt menar jag att man beräknar själva integralen för flödet genom ytan. Man gör ingen omskrivning med gauss sats. Förresten, skulle du kunna skicka facit?
Lasse Vegas skrev:Med vanligt menar jag att man beräknar själva integralen för flödet genom ytan. Man gör ingen omskrivning med gauss sats. Förresten, skulle du kunna skicka facit?
Ja jag kan absolut skicka,men de hoppar över många steg och jag ser inte hur saker blir till något annat osv. Jag tycker inte lösningen är utförlig som jag hade önskat.

Aa de utökar med en cirkelskiva för att bilda ett halvklot i facit.
Lasse Vegas skrev:Aa de utökar med en cirkelskiva för att bilda ett halvklot i facit.
Jaa och det förstår jag inte varför. Se #22
Har du en skål och en tallrik tillgänglig?
En annan sak som jag inte förstår är varför N=(0,0,-1) samt hur man kommit dit? Sen är det många saker som är oklart för mig i facit.
Lasse Vegas skrev:Har du en skål och en tallrik tillgänglig?
Nej tyvärr jag är inte hemma.
Lasse Vegas skrev:Man behöver inte utöka det med en halfsvär utan kan göra en sluten yta genom att lägga till en cirkelskiva på botten.
Nedre ytans enhetsnormal är ju dessutom bara .
Skivan ligger i xy-planet och har en enhetsnormal som är riktad rakt ner dvs i negativ z-riktning
destiny99 skrev:Lasse Vegas skrev:Har du en skål och en tallrik tillgänglig?
Nej tyvärr jag är inte hemma.
Har du två händer?
Lasse Vegas skrev:Lasse Vegas skrev:Man behöver inte utöka det med en halfsvär utan kan göra en sluten yta genom att lägga till en cirkelskiva på botten.
Nedre ytans enhetsnormal är ju dessutom bara .
Skivan ligger i xy-planet och har enhetsnormalen N = -k
Har det att göra man vill hitta flödet upp till z>=0 dS pekar utåt och då har vi (df/dx,df/dy,df/dz) eller jag kanske bara rör till det..
Lasse Vegas skrev:destiny99 skrev:Lasse Vegas skrev:Har du en skål och en tallrik tillgänglig?
Nej tyvärr jag är inte hemma.
Har du två händer?
Beror på vad du undrar om
Det går ju att räkna på det och komma fram till enhetsnormalen, men det är ju också lätt att se bestämma den utan beräkning. Enhetsnormalen är vinkelrät mot ytan, eftersom cirkelskivan ligger i xy-planet så är vinkelrät riktning z-riktning.
Lasse Vegas skrev:Det går ju att räkna på det och komma fram till enhetsnormalen, men det är ju också lätt att se bestämma den utan beräkning. Enhetsnormalen är vinkelrät mot ytan, eftersom cirkelskivan ligger i xy-planet så är vinkelrät riktning z-riktning.
Jag föredrar att beräkna enhetsnormalen. Hur beräknar man den ? Jag har lite svårt att se vad som är ytan och om cirkelskivan utgör ytan tillsammans med halvsfären.
destiny99 skrev:Lasse Vegas skrev:destiny99 skrev:Lasse Vegas skrev:Har du en skål och en tallrik tillgänglig?
Nej tyvärr jag är inte hemma.
Har du två händer?
Beror på vad du undrar om
Du får låtsas att händerna är halvsfären och cirkelskivan. Gör en av händerna skålformade, den handen representerar halvsfären (x^2 + y^2 + z^2 = 1, z >= 0). Låt andra handen representera cirkelskivan (x^2 + y^2 <= 1, z = 0). Om du nu täcker för skål-handen med cirkelskiva-handen får du en sluten yta. Området som innesluts är x^2 + y^2 + z^2 <= 1, z >= 0.
Lasse Vegas skrev:destiny99 skrev:Lasse Vegas skrev:destiny99 skrev:Lasse Vegas skrev:Har du en skål och en tallrik tillgänglig?
Nej tyvärr jag är inte hemma.
Har du två händer?
Beror på vad du undrar om
Du får låtsas att händerna är halvsfären och cirkelskivan. Gör en av händerna skålformade, den handen representerar halvsfären (x^2 + y^2 + z^2 = 1, z >= 0). Låt andra handen representera cirkelskivan (x^2 + y^2 <= 1, z = 0). Om du nu täcker för skål-handen med cirkelskiva-handen får du en sluten yta. Området som innesluts är x^2 + y^2 + z^2 <= 1, z >= 0.
Det gick tyvärr inte så bra.
Okej, vi provar det här. Tänk dig att vi kollar på halvsfären från sidan. Det kan se ut något såhär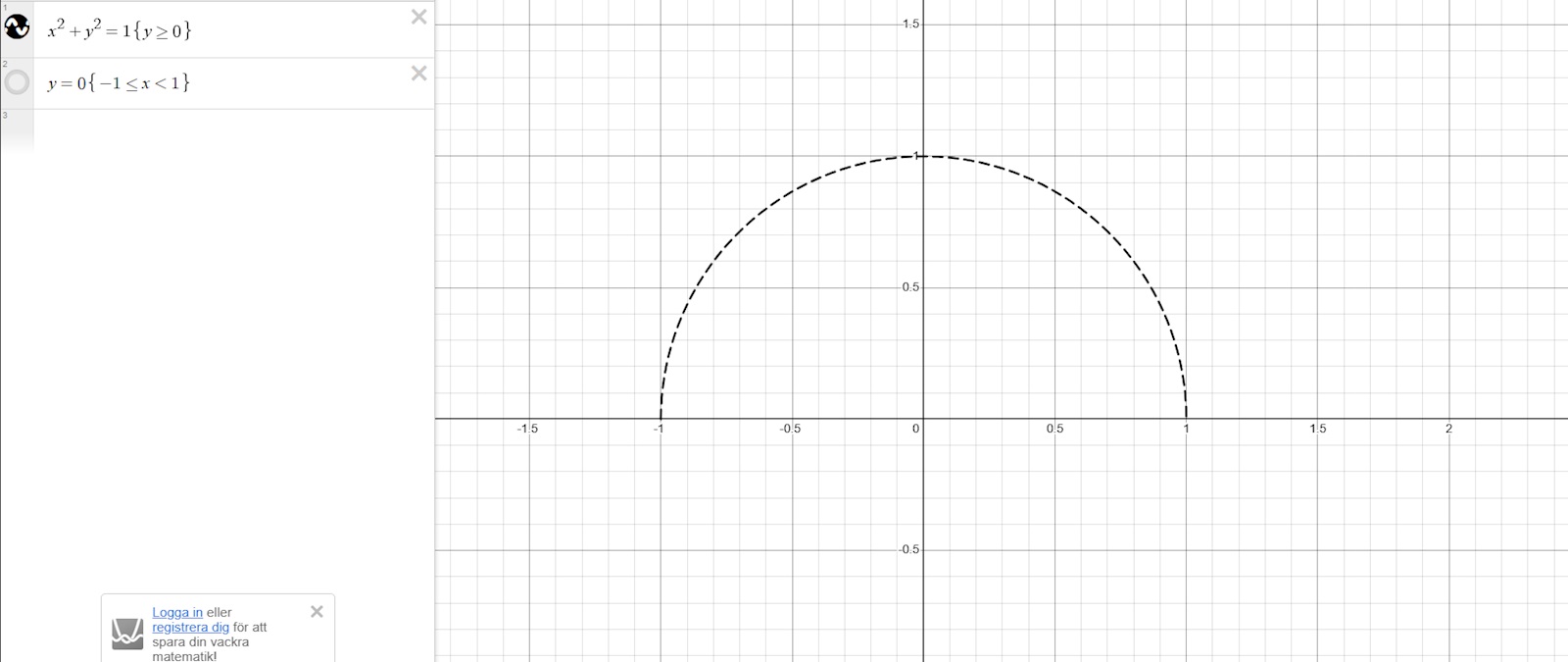 När vi sätter dit cirkelskivan så kopplar vi ihop punkterna (-1, 0) och (1, 0) och får
När vi sätter dit cirkelskivan så kopplar vi ihop punkterna (-1, 0) och (1, 0) och får
Halvsfären representeras av halvcirkeln, och cirkelskivan av prickade linjen
Lasse Vegas skrev:Halvsfären representeras av halvcirkeln, och cirkelskivan av prickade linjen
Okej
Får du en tydligare bild?
Lasse Vegas skrev:Får du en tydligare bild?
Ja helt ok eftersom det är svårt att tänka i 3D. Men jag köper den figuren i alla fall.
Ska vi gå igenom hur man ska beräkna detta då? Då har vi totala flöde för halvsfär+cirkelskivan och tillsammans utgör de en sluten flöde eller vad man ska säga. Hm jag kanske frågar AI istället eftersom den fick samma svar som facit tidigare.
Man ska vara försiktig med ChatGPT eftersom den ibland har fel. Men yeah prova att utföra uträkningen.
I facit så är det HL här som ska beräknas vilket består av två integraler 
Lasse Vegas skrev:Man ska vara försiktig med ChatGPT eftersom den ibland har fel. Men yeah prova att utföra uträkningen.
I facit så är det HL här som ska beräknas vilket består av två integraler
Ja precis jag förstår inte dock detta. Så jag kan inte utföra beräkningar på något jag inte förstår.
Det kan man dock göra, du kan fortfarande beräkna integralerna även fast du inte förstår. Du kan prova att lösa uppgiften och se om det klickar längs vägen.
Lasse Vegas skrev:Det kan man dock göra, du kan fortfarande beräkna integralerna även fast du inte förstår. Du kan prova att lösa uppgiften och se om det klickar längs vägen.
Jag tror inte jag förstår integralerna eller alltså vad som är vad samt varför det står som det gör tex u*(0,0,-1). Vad menas med (0,0,-1) ? Var kommer den ifrån? Hur får man fram till den? Hur bestämmer vi gränserna? Varför subtraherar vi ?
Sen om du känner att du behöver lära dig mer om hur det funkar så kanske det blir lättare eftersom du på något sätt har utfört själva beräkningarna och sätt hur man löser uppgiften.
destiny99 skrev:Lasse Vegas skrev:Det kan man dock göra, du kan fortfarande beräkna integralerna även fast du inte förstår. Du kan prova att lösa uppgiften och se om det klickar längs vägen.
Jag tror inte jag förstår integralerna eller alltså vad som är vad.
Det är lite jobbigare i så fall
Ser gränserna rätt ut för vinklarna? Jag räknar ut integralen för totala ytan eller ska man bara tänka att vi räknar volymen av en halvsfär? Sen vore det bra om jag fick svar på min fråga i #48 där jag redigerat inlägget. 
destiny99 skrev:Lasse Vegas skrev:Det kan man dock göra, du kan fortfarande beräkna integralerna även fast du inte förstår. Du kan prova att lösa uppgiften och se om det klickar längs vägen.
Jag tror inte jag förstår integralerna eller alltså vad som är vad samt varför det står som det gör tex u*(0,0,-1). Vad menas med (0,0,-1) ? Var kommer den ifrån? Hur får man fram till den? Hur bestämmer vi gränserna? Varför subtraherar vi ?
(0, 0 , -1) är cirkelskivans enhetsnormal. Jag minns inte hur man bestämmer den algebraiskt, bör vara att man tar kryssprodukten av ytans partiella derivator eller något sådant. Som sagt, minns inte 100%. Går också att resonera att cirkelskivan ligger i xy-planet och har en enhetsnormal som är i negativ z-riktning.
Vi subtraherar integralen eftersom den utgörs av själva utökningen. Gauss sats fungerar om vi utökar området till ett slutet område, men när vi utökar ändras uttrycket och det måste vi kompensera för det genom att ta bort utökningen.
Lasse Vegas skrev:destiny99 skrev:Lasse Vegas skrev:Det kan man dock göra, du kan fortfarande beräkna integralerna även fast du inte förstår. Du kan prova att lösa uppgiften och se om det klickar längs vägen.
Jag tror inte jag förstår integralerna eller alltså vad som är vad samt varför det står som det gör tex u*(0,0,-1). Vad menas med (0,0,-1) ? Var kommer den ifrån? Hur får man fram till den? Hur bestämmer vi gränserna? Varför subtraherar vi ?
(0, 0 , -1) är cirkelskivans enhetsnormal. Jag minns inte hur man bestämmer den algebraiskt, bör vara att man tar kryssprodukten av ytans partiella derivator eller något sådant. Som sagt, minns inte 100%. Går också att resonera att cirkelskivan ligger i xy-planet och har en enhetsnormal som är i negativ z-riktning.
Vi subtraherar integralen eftersom den utgörs av själva utökningen. Gauss sats fungerar om vi utökar området till ett slutet område, men när vi utökar ändras uttrycket och det måste vi kompensera för det genom att ta bort utökningen.
Jag får kolla upp detta med kursare /PA livehjälp och liknande gällande enhetsnormalen ( varför den är som den är så man minns detta väl). Justnu kan jag bara acceptera att det är så.
Det här får jag för integralen av hela området.


Det verkar inte bli rätt. Jag misstänker att det är pga gränserna,hur ska man tänka kring phi och theta? Jag valde att theta går från 0 till 2pi om man tänker på botten cirkeln och sen theta från 0 till pi/2.