För vilka a är vektorerna linjärt oberoende? (Matematik/Universitet)

Det du skriver om determinanter stämmer mycket väl. Om du sätter att $A = [v_{1}, v_{2}, v_{3}]$ med vektorerna som kolonn- eller radvektorer, så kan du hitta de a:n där vektorerna är linjärt oberoende. :)

Jag sätter

$A = [\begin{matrix} 1 & 1 & 1 \\ 1 & 2 & a + 2 \\ 1 & a + 1 & 1 \end{matrix}]$ .

Ska jag nu utföra radoperationer för att få matrisen på trappstegsform?

...

Jag fick fram denna matris på trappstegsform:

$[\begin{matrix} 1 & 1 & 1 \\ 0 & 1 & a + 1 \\ 0 & 0 & - a - 2 \end{matrix}]$ . EDIT: Detta visade sig vara felaktigt.

Vi har nu nått trappstegsform och kan därför beräkna determinanten som produkten av diagonalen: 1*1*(-a-2) = -a-2.

Då vet vi att när a=-2 så är determinanten lika med 0.

För att vektorerna ska vara oberoende gäller alltså att a≠ -2.

EDIT: Sarrus regel visade i stället att determinanten är lika med 0 när a= -1.

Och hur ska jag få fram för vilka värden på a som vektorerna är linjärt oberoende?

Det kan väl inte vara för alla a ≠ -1?

Antingen använder du radoperationer, eller så beräknar du determinanten direkt. Nu kan du dock beräkna determinanten direkt, när är den nollskild? För vilka a utgör vektorerna en bas?

Smutstvätt skrev:
Antingen använder du radoperationer, eller så beräknar du determinanten direkt. Nu kan du dock beräkna determinanten direkt, när är den nollskild? För vilka a utgör vektorerna en bas?

Determinanten är nollskild för alla reella tal a som inte är -1.

Vi har att när a≠-1 så är vektorerna $v_{1}, v_{2} o c h v_{3}$ oberoende och då utgör de en bas i rummet.

Återstår nu att ta reda på koordinaterna för vektorn $\vec{u}$ =(2a, a, 0) i basen $v_{1}, v_{2}, v_{3} .$

Hur löser jag detta?

Lisa Mårtensson skrev:
Smutstvätt skrev:
Antingen använder du radoperationer, eller så beräknar du determinanten direkt. Nu kan du dock beräkna determinanten direkt, när är den nollskild? För vilka a utgör vektorerna en bas?
Determinanten är nollskild för alla reella tal a som inte är -1.
Vi har att när a≠-1 så är vektorerna $v_{1}, v_{2} o c h v_{3}$ oberoende och då utgör de en bas i rummet.
Återstår nu att ta reda på koordinaterna för vektorn $\vec{u}$ =(2a, a, 0) i basen $v_{1}, v_{2}, v_{3} .$
Hur löser jag detta?

Du kan ju sätta upp u=(2a, a, 0) =c₁*v₁+c₂*v₂+c₃*v₃ Du får tre ekvations system såhär. c_i i=1,2,3 är konstanter.

Tack! Hur kan nu detta ekvationssystem komma att se ut? Några ledtrådar?

Jag förstår det som att $c_{1}, c_{2}, c_{3}$ kommer att utgöra koordinaterna. Har jag fattat rätt?

Lisa Mårtensson skrev:
Tack! Hur kan nu detta ekvationssystem komma att se ut? Några ledtrådar?
Jag förstår det som att $c_{1}, c_{2}, c_{3}$ kommer att utgöra koordinaterna. Har jag fattat rätt?

c₁ c₂ c₃ kommer att vara koefficienterna framför basvektorerna v₁ , v₂ och v₃.

2a=c₁*1+c₂*1+c₃*1
a= c₁*1+c₂*2+c₃*(a+2)
0=c₁*1+c₂*(a+1)+c₃*1
u=A*C där A är matrisen [v₁ v₂ v₃] och C är en vektor (c₁, c₂ , c₃) som har koefficienterna i sig.

Och ja det blir koordinaterna. c₁ är hur långt du ska gå i v₁ riktningen c₂ är hur långt du ska gå i v₂ riktningen och c₃ är hur långt du ska gå i v₃ riktningen.

Sarrus regel ger att determinanten är noll när a=-1 och när a=0.

Då vet vi att för alla $a \neq - 1 o c h a \neq 0$ är vektorerna (1, 1, 1), (1, 2, a+1) samt (1, a+2, 1) linjärt oberoende och bildar en bas i rummet.

Förstadelen av uppgiften är färdiglöst.

Egocarpo skrev:

Du kan ju sätta upp u=(2a, a, 0) =c₁*v₁+c₂*v₂+c₃*v₃ Du får tre ekvations system såhär. c_i i=1,2,3 är konstanter.

Kommentar från Lisa Mårtensson:
Får man inte ETT ekvationssystem med TRE obekanta?
Ser min uppställning bra ut?

Har jag nu bara kvar att lösa ekvationssystemet för att få fram koordinaterna för vektorn u i basen $v_{1}, v_{2}, v_{3}$ ?

Jag har en systemmatris och en lösningsvektor och vill få ut vad $c_{1}, c_{2} o c h c_{3}$ är.

(I många fall brukar man kalla variablerna x, y, z.)

Systemmatrisen A är matrisen [ $v_{1}, v_{2}, v_{3}$ ] och lösningsvektorn utgörs av koordinaterna i vektorn $\vec{u}$ :

$[\begin{matrix} 1 & 1 & 1 \\ 1 & 2 & a + 2 \\ 1 & a + 1 & 1 \end{matrix}] [\begin{matrix} 2 a \\ a \\ 0 \end{matrix}]$ .

Lisa Mårtensson skrev:
Har jag nu bara kvar att lösa ekvationssystemet för att få fram koordinaterna för vektorn u i basen v1, v2, v3?

Prova! Du kan ju alltid se sen om det stämmer.

Jag försöker att få systemet på reducerad trappstegsform och läsa av lösningarna i HL, men det är svårt att reducera alla a tycker jag.

Jag skulle alltså vilja ha systemet så här:

$|\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}| |\begin{matrix} l ö s n i n g f ö r c_{1} \\ l ö s n i n g f ö r c_{2} \\ l ö s n i n g f ö r c_{3} \end{matrix}|$ , men det verkar alltså svårt att få till det så.

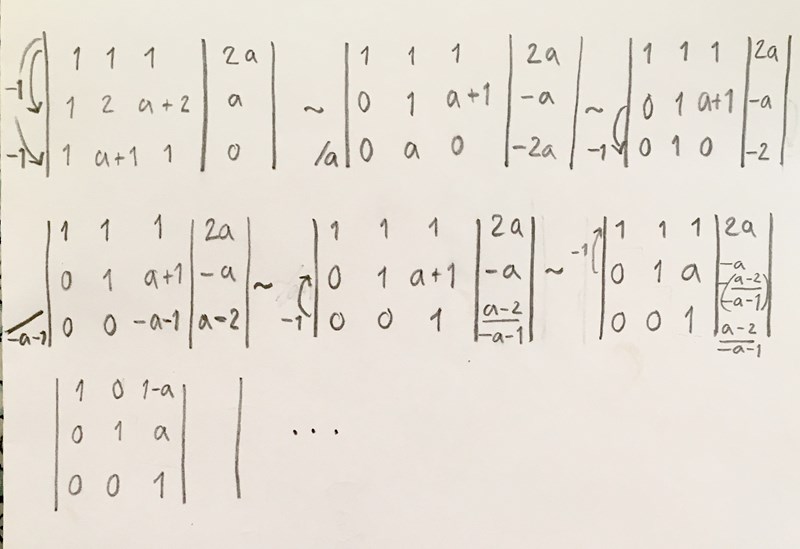
Skulle det kanske vara intressant att sätta in ett värde på a (som ej är -1 eller 0) och se vad det blir för lösningar.

Jag kunde för enkelhetens skull prova med att sätta a=1.

Varför inte ta R1-R3 och R2-a*R3 innan du tar R1-R2 i det sista steget du genomfört? På så sätt slipper du 1-a i första raden.

Är det inte när vektorerna är linjärt oberoende som det är intressant?

Hmm men man delar med noll i så fall och det är ju inte bra.

Sarrus regel ger att determinanten är noll när a=-1 och när a=0.

Då vet vi att för alla a≠−1 och a≠0a≠-1 och a≠0 är vektorerna (1, 1, 1), (1, 2, a+1) samt (1, a+2, 1) linjärt oberoende och bildar en bas i rummet.

Då är vektorerna linjärt oberoende för alla a som inte är -1 eller 0. Därför menar jag att man skulle kunna sätta in ett värde på a som inte är något av dessa, t.ex. 1.

...

Nä, dela med noll får namn ju inte göra.

Men om man delar alla element i en rad med något och några av elementen är noll så är det väl ok? Man vill kanske dela 1-a med sig själv för att få 1. Då kanske de andra operationerna består i att man delar 0 med 1-a och då får man fortfarande noll. Är det ok att göra så när man utför radoperationer?

Att sätta in a=1 och sedan lösa systemet ger bara den entydiga lösningen för det a:t, och inte en mer allmän lösning i termer av a.

Jag tror det som gör det svårt för dig att bli av med a:na är att du inte har dragit någon multipel av a av en rad från en annan vilket resulterar i att du "flyttar runt" dem. Om vi utgår från matrisen du har efter sista steget, dvs.

$[\begin{matrix} 1 & 0 & 1 - a \\ 0 & 1 & a \\ 0 & 0 & 1 \end{matrix}]$

,är du bara två radoperationer från reducerad trappstegsform. Ta R1-(1-a)R3->R1 så får du i sista kolonnen (1-a)-(1-a)=1-1-a+a=0 och tar du R2-(a)R3->R2 får du a-a=0.

Tack så mycket doubledumb. Jag ska göra så.

Innan jag läste ditt svar hade jag testat att räkna på fallet att a=1. Men jag förstår att det inte ger svaret på andra halvan av uppgiften vad gäller vektorn u i basen v.

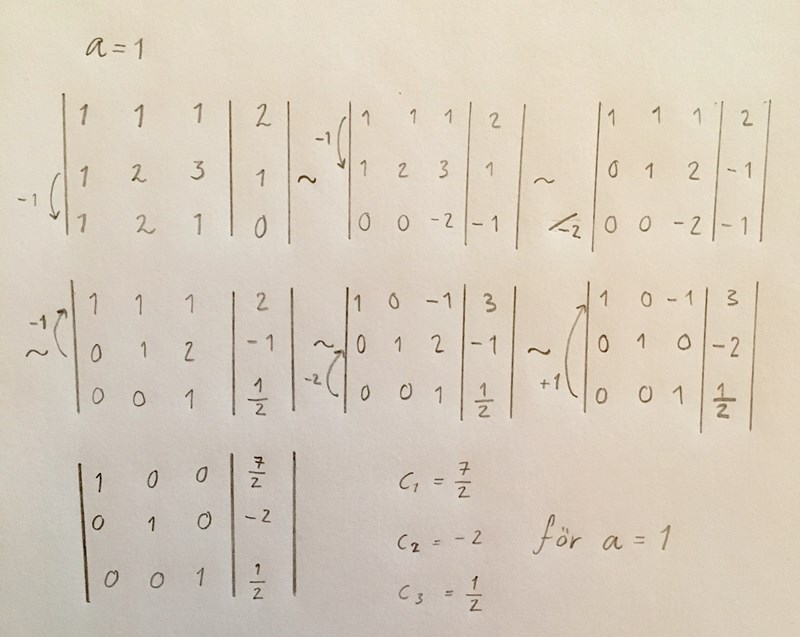
doubledumb skrev:
Att sätta in a=1 och sedan lösa systemet ger bara den entydiga lösningen för det a:t, och inte en mer allmän lösning i termer av a.
Jag tror det som gör det svårt för dig att bli av med a:na är att du inte har dragit någon multipel av a av en rad från en annan vilket resulterar i att du "flyttar runt" dem. Om vi utgår från matrisen du har efter sista steget, dvs.
$[\begin{matrix} 1 & 0 & 1 - a \\ 0 & 1 & a \\ 0 & 0 & 1 \end{matrix}]$
,är du bara två radoperationer från reducerad trappstegsform. Ta R1-(1-a)R3->R1 så får du i sista kolonnen (1-a)-(1-a)=1-1-a+a=0 och tar du R2-(a)R3->R2 får du a-a=0.

Jag förstår hur du menar i VL, hur jag ska få bort a:na. Men blir det inte väldigt komplicerat i HL?

Skulle du möjligen vilja visa hur det skulle bli i lösningsvektorn? Jag är inte så van vid att dra bort en multipel av något av en rad från en annan rad. Det blir så lätt fel.

Ja, det blir lite komplicerat i VL. Enligt Wolfram Alpha ska du få

$[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} \frac{2 a^{2} + 5 a}{a + 1} \\ - 2 \\ - \frac{a + 2}{a + 1} \end{matrix}]$

Ser ut som att det blivit fel i HL i sista raden. Möjligtvis går det att fixa genom att skriva -a-1 som -(a+1). Då blir det rätt i nämnaren, i alla fall.

Ett förslag är att fortsätta lösa systemet som ett vanligt ekvationssystem efter du nått trappstegsform (1:or diagonalt, 0:or under, vad som helst över). Det visade sig vara lite enklare, förutsatt att du har rätt i sista raden.

Tack så jättemycket!

$c_{1} = \frac{2 a^{2} + 5 a}{a + 1} c_{2} = - 2 c_{3} = \frac{2 - a}{a + 1}$

Och det är därmed de sökta koordinaterna för vektorn u.