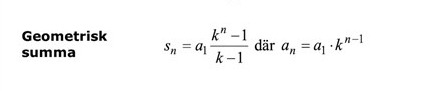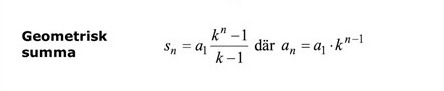För vilka heltal n gäller...
Min fråga:
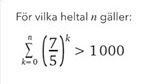
Jag har löst uppgiften nästan som i lösningen, men jag förstår inte varför de skriver n+1 istället för n.
Lösning:

De använder summaformeln för en geometrisk serie, som säger att:
Summan kan skrivas som .
Så det är därför de skriver som exponent. :)
Men i mitt formelblad står det inte n+1 som exponent, bara n, som jag också använt för andra uppgifter
Anna000 skrev:Men i mitt formelblad står det inte n+1 som exponent, bara n, som jag också använt för andra uppgifter
Kan du visa en bild på formelsamlingen. Det hela beror på hur man numrerar index och antalet termer i summan. Det kan skilja sig åt hur denna summa ser ut beroende på hur den framställs.
Anna000 skrev:
OK. Formeln är sann då sista talet i summan är a_1 k^(n-1), men ditt sista tal är a_1 k^n, d.v.s. "1 större". Därför skall du använda n+1 i formeln istf n.
är det för att i slutet av summatecknet det står "n"?
Anna000 skrev:är det för att i slutet av summatecknet det står "n"?
ja, att det slutar på ak^n