för vilket värde på x är uttrycket ej definerat.

Är jag på rätt bana ?

Tänk på att uttryck bara är definerade då då nämnaren inte är lika med 0 

ok hade det funkat att ta nämnarens konjugat ?

Försök hitta vilka x som gör så att nämnarna är 0 utan att förändra utrycket. 

kan jag tänka så här $$\begin{gathered} \sin \left(x\right)\ne 0 x\ne 1 \\ \cos \left(x\right)\ne 0 x\ne 0 \end{gathered}$$

För att nämnaren ska bli 0 måste sinx+cosx =0

Dvs sinx = - cos x.

För vilka x gäller det?

kan man kika på enhetscirkeln ?

-cos(x)=sin(x+270) litet tips, glöm inte period. 

jag har ej kommit till avsnittet om trig funktioner och perioder än

Ture skrev:

För att nämnaren ska bli 0 måste sinx+cosx =0

Dvs sinx = - cos x.

För vilka x gäller det?

är inte lösningen tanx=-1 ?

Kan det det här vara ett bra svar ? 

Trigonometriska funktioner har en period vilket betyder att dem repeterar alltså att sin(x)=sin(x+360*n) då n är ett heltal, tänk att den gör en full rotation i enhetscirkeln, därfär om man vill ha alla lösningar måste man sätta dit 360*n då n är ett heltal. 

Ditt svar är orelevant för frågan vill ha när funktionen är odefinerad alltså då nämnaren i någon eller båda bråken är noll.

jag vet nte hur jag kan hitta det eller hur jag kan ställa upp uttrycket/ funktionen som ger mig lösningen ?

Första bråkets nämnare är sin(x)+cos(x) som då ska vara lika med noll för att funktionen ska vara odefinerat så sin(x)+cos(x)=0 sin(x)=-cos(x) , i det andra bråket är det då cos(x)=0, nu får vi försöka lösa dessa ekvationer.

kan jag arsin och arcos för att lösa x ?

ja, men glöm inte de olika trigonometriska identiteterna som cos(-x)=cos(x) sin(x+270)=-cos(x) sin(180-x)=sin(x) och period på 360*n då n är ett heltal.

jag undrar måste man ha med trig identiterna så länge man har med funktionernas period dvs:

$$\begin{gathered} \sin \left(x\right)=\sin (x+n\times 360) \\ \cos \left(x\right)=\cos (x+n\times 360) \end{gathered}$$

Du måste använda trig identitieter för perioden visar inte alla lösningar.

När man håller på med att lösa uppgift 1222c i boken Matematik 5000+, kurs 4, så har man ännu inte sett trigonometriska ekvationer där den obekanta variabeln förekommer innanför flera trigonometriska funktioner.

Uppgiften 1222c handlar om att visa att likheten gäller för alla x där uttrycken är meningsfulla och din lösning i #12 besvarar uppgiftens frågeställning.

Uppgiften frågar egentligen inte för vilka $x$ alla uttrycken är definierade. Å andra sidan är det god kutym att faktiskt undersöka detta. Kravet här är att man inte får dividera med noll, så man ska undersöka för vilka $x$ det inträffar att man skulle begå brottet att dividera med noll.

De problematiska x fås alltså genom att lösa ekvationen:

• $\sin x + \cos x = 0$ (sådana x är förbjudna i VL) och
• $\cos x = 0$ (sådana x är förbjudna i HL).

(Dessutom ska $\tan x$ vara definierad i VL, vilket i sig innebär att $\cos x = 0$ är förbjudet.)

Den första ekvationen kan skrivas om som $\tan x = -1$ vilket du helt rätt skrivit i #11. Lös ut $x$ ur dessa ekvation (se Exempel 3 och rutan längst ner på sid 16 eller den lösta uppgiften 1127).

Den andra ekvationen ekvationen löses som i Exempel 2 och rutan i mitten på sid 16 (eller lösta uppgiften 1128)

LuMa 07 skulle visa lösningen hur de övriga menar. Jag verkar inte riktigt fatta hur de vill. 

Jag har inte kommit så långt på trig än.

Låt oss titta på hur man löser $\sin x + \cos x = 0$ utan att byta till tangens.

Man utnyttjar sambandet mellan en trig. funktion och dess co-funktion för komplementvinkeln

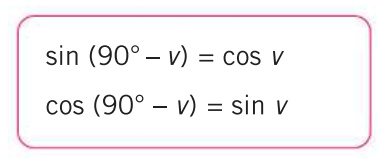
(sid 21 i kursboken).

Man kan alltså byta ut $\cos x$ i ekvationen mot $\sin(90^\circ - x)$. På så sätt får man att

$\sin x + \cos x = 0 \iff \sin x + \sin(90^\circ - x) = 0 \iff \sin x = -\sin(90^\circ - x)$.

Nu kan man skriva om HL genom att utnyttja att sinus är en udda funktion (minustecknet framför sinus kan flyttas in i sinus)

(sid 20 i kursboken)

Man får därmed $\sin x = -\sin(90^\circ - x) \iff \sin x = \sin ( - (90^\circ - x) ) \iff \sin x = \sin(x-90^\circ)$. Sedan vet man att sinusvärdet bevaras för supplementvinkeln.

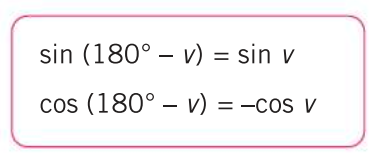
(sid 20 i kursboken)

Ekvationen $\sin x = \sin(x-90^\circ)$ kan alltså lika gärna skrivas $\sin(180^\circ - x) = \sin(x-90^\circ)$. Man får alltså två lösningsskaror:

• $x = x-90^\circ + n\cdot 360^\circ$ som saknar lösningar. (Det är x som ska lösas ut)
• $180^\circ - x = x-90^\circ + n\cdot 360^\circ$, vilket ger $x = 135^\circ + n\cdot 180^\circ$, där $n$ är ett godtyckligt heltal

(Jämför gärna detta med lösningarna till grundekvationen för sinus på sid 16).

Nu har man alltså tagit reda på att $x = 135^\circ + n\cdot 180^\circ$ är förbjudna.

Det återstår att undersöka $\cos x = 0$, men det kan du göra exakt på samma sätt som Exempel 2 / grundekvation för cosinus på sid 16. Då får du att $x = \pm 90^\circ + n\cdot 360^\circ$ är förbjudna.