Fördelningsfunktionsmetoden

Om du släpper att det råkar ligga lite statistik runt, bara tittar direkt på frågan och räknar ut värdemängden för u som i gymnasiet, vad får du då?

Bortser man från statistiken kan ju u anta vilka värden som helst.

Du vet att y är mellan 0 och 1.

Hej,

Kravet på $Y$ ger att $e^{-u/\omega}$ ska ligga mellan 0 och 1, vilket ger dig den sökta täthetsfunktionens $f(u)$ definitionsmängd. 

Integralen från 0 till F(u) är fel och dessutom irrelevant; tätheten för Y är konstant 1, inte linjär som du skriver. Du har redan bestämt cdf för U i tidigare beräkningar. 

Ah, okej! Undersökte integralen eftersom jag var osäker på definitionsmängden just. Ser också att jag har gjort fel; $e^{-\frac{u}{\omega }}$ ska det ju stå för $F_U\left(u\right)$.

Och jag förstår ju vad som ställer till det för mig; att $\omega$> 0

Jag fick något iaf, vet inte om det är rätt.

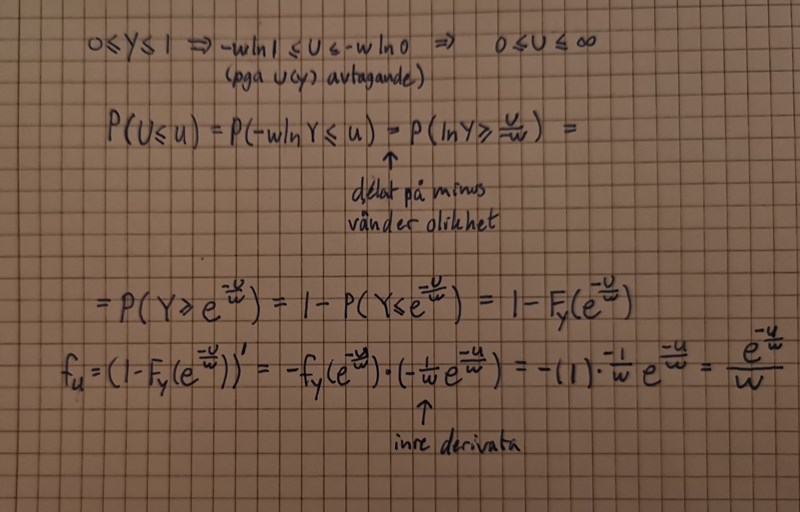
Hej,

Slumpvariabeln $Y$ är likformigt fördelad på intervallet [0,1]; det betyder att dess fördelningsfunktion är $F_{Y}(y) = y$ då $y \in [0,1]$.

Slumpvariabeln $U$ har följande fördelningsfunktion.

    $F_{U}(u) = P(U \leq u) = P(\ln Y \geq -\frac{u}{\omega}) = 1-P(\ln Y \leq -\frac{u}{\omega})\\ = 1-P(Y \leq e^{-\frac{u}{\omega}}) = 1-F_Y(e^{-\frac{u}{\omega}}) = 1-e^{-\frac{u}{\omega}};$

notera att olikheten byter riktning på grund av division med det negativa talet $-\omega$ och att exponentialfunktionen $x\mapsto e^{x}$ är strängt växande.

Beräkningen visar att slumpvariabeln $U$ är exponentialfördelad med intensiteten $1/\omega$ vilket medför att dess väntevärde är $\mathbb{E}(U)=\omega$ och varians $\text{Var}(U) = \omega^2.$ Täthetsfunktionen är därför $f_U(u) = \frac{1}{\omega}e^{-u/\omega}.$

Momentgenererande funktionen (mgf) är

    $\displaystyle m_U(s) = \mathbb{E}(e^{sU}) = \int_{u=0}^\infty \frac{1}{\omega}e^{-(\frac{1}{\omega}-s)u} \,du = ...$

Okej, tack båda två! Det här var inte helt lätt, som jag först trodde. Men jag hoppas kunna lösa det nu iaf!