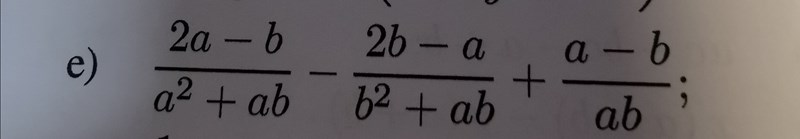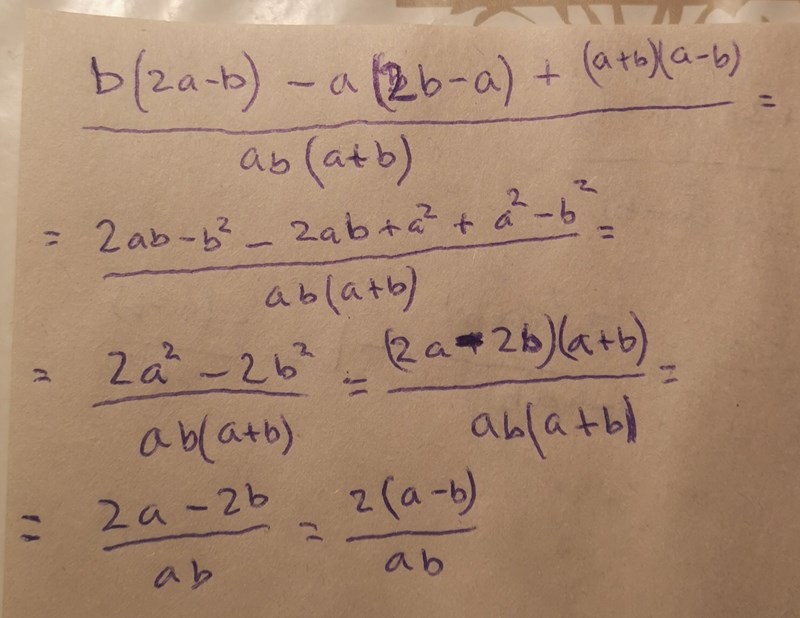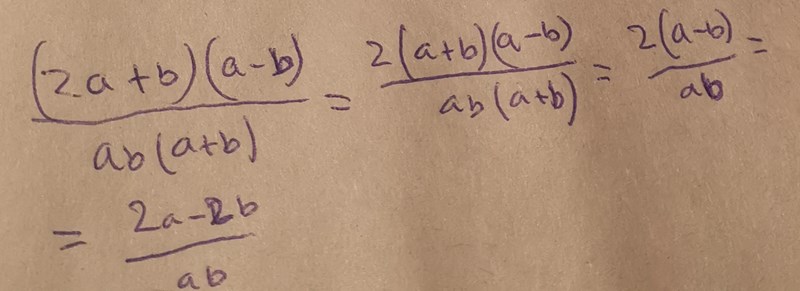Vad blir den gemensamma nämnaren?
Bryt ut a ur första nämnaren och b ur andra nämnaren. Ser du bättre hur du skall göra?
Nej tyvärr. Jag har fastnat på första steget. ☹️
Börja med att faktorisera alla nämnare. Visa hur det ser ut när du har gjort det.
Vad gör du för att komma från andra till tredje raden? I den första termen ser jag att du förkortar bort a (men jag vet inte varför), men vad är det du gör i den andra termen?
Du har tre olika termer i nämnarna, två i vardera av bråken. För läng hela ekvationen med ab(a+b). Du kommer att bli av med alla krångliga nämnare. Visa hur det ser ut när du har gjort detta.
Jag förstår inte vad du menar?
Vad är det du inte förstår? Vet du hur du skall göra för att multiplicera hela ekvationen (båda sidor) med ab(a+b)? Du borde ha lärt dig det i Ma1.
EDIT: Jag läste fel. Det var ett plus mellan andra och tredje termen inte ett likhetstecken. Man blir inte av med nämnarna.
Jag förstår inte hur den minsta gemensamma nämnaren bli ab(a+b).
Ska jag multiplicera första nämnaren med b, andra nämnaren med a, och tredje nämnaren med (a+b)?
Är du med på att MGN till är ab?
Ja. 100%
Är du med på att MGN till är ab(a+b)?
Jo. För att nämnarna ska bli lika, då måste vi multiplicera med respektive bokstav. B i första nämnaren och a i andra nämnaren.
Och det blir b*a(a+b), a*b(a+b). Lika.
Och då om vi vill ha tredje nämnaren lika, då måste vi multiplicera ab med (a+b).
Sen löser det sig. 🙂🦉