Förenkla Potensekvation
Hej!
Har det struligt i hjärnan när det kommer till att förenkla en Potensekvation, får inte till det..
Uppgiften:
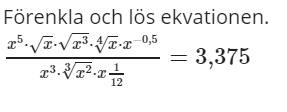
Det jag försöker göra är att addera ihop täljaren och nämnarens alla roten ur och upphöjningar, och sedan multiplicera minsta gemensamma nämnare för få bort termen innan x och sedan lösa ut HL
Med detta får jag svar ungefär x=2,75
Som ni ser rör jag ihop det rejält, rätta svaret är x=1,5.
Kändes inte rätt när jag försökte lösa ekvationen, dels för allt jag gjorde i VL gjorde jag inte med HL, men ska man verkligen göra det när man bara förenklar roten ur och upphöjningarna?
Lite hjälp på vägen, vore grymt!
Tack
Det verkar som det blivit något galet i formateringen. Jag antar att en tolftedel i nämnaren skall vara en exponent till :et bredvid, d.v.s.
Jag förstår inte riktigt hur du har tänkt, men som du själv konstaterat har det blivit fel. Däremot är din generella metod korrekt, du skall förenkla i VL tills du får en enkel ekvation. Jag skulle arbeta i bråkform:
Nu när du skall förenkla VL rekommenderar jag att du omvandlar rötterna till rena potenser. Exempelvis har du ju att:
och
Kan du göra på samma sätt med resten av rötterna? Vad får du då?
Hur fick du 8,7 som exponent?
1. Börja med att göra om alla roten ur tecken till upphöjt (t.ex. kvadratrot är samma som upphöjt med 1/2).
2. Addera täljarens exponenter med varandra, och addera nämnarens exponenter med varandra.
3. Subtrahera exponenten i nämnaren från exponenten i täljaren.
lite otydlig bild:
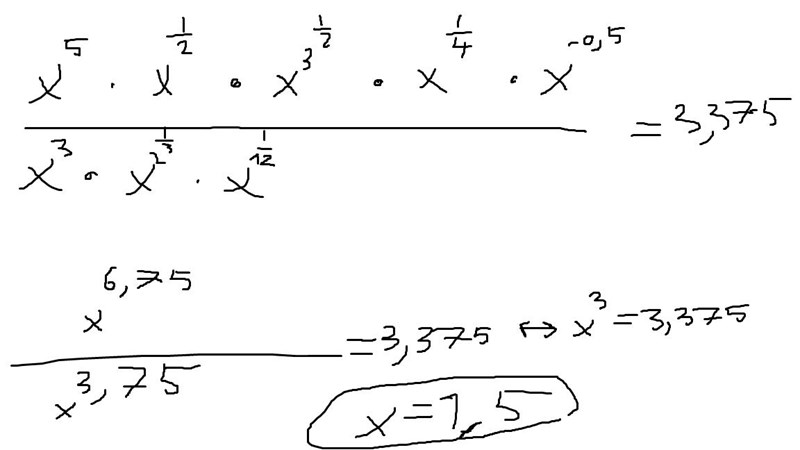
Wow! Tack för snabb respons!
Det stämmer nog, att 1/12 är en exponent, vi får anta det.
Den där behövdes, jag har rört ihop det och istället för höja upp med 1/2 för räkna roten ur, så har jag höjt upp med 2 för ta bort den.
Så istället för tänkte jag .
Laguna:
Det vågar jag inte svara på, kliar mig om huvudet och funderar själv på hur fasiken jag fick 8,7 som exponent :s Blir så ibland när man gräver sig för djupt i ekvationen hehe.
Då försöker jag igen:
Kommit fram till att jag vill få upphöjt till 9 i nämnaren så jag får
Och misstänker ett fel jag gör är
Uschh för potenser :((
Iridiumjon skrev:1. Börja med att göra om alla roten ur tecken till upphöjt (t.ex. kvadratrot är samma som upphöjt med 1/2).
2. Addera täljarens exponenter med varandra, och addera nämnarens exponenter med varandra.
3. Subtrahera exponenten i nämnaren från exponenten i täljaren.
lite otydlig bild:
Oj nu när jag ser din uträkning, vad sysslar jag med egentligen :s
Det är potenslagarna som jag har svårt med
Denna regel jag föll på, nu när jag försökte igen på pappret och följde så fick jag till det med samma resultat som Irdiumjon!
Tack hörni
I mina ögon står det x gånger en tolftedel i frågan, inte x upphöjt till en tolftedel. Dåligt typsatt.
Jag kan annars rekommendera att räkna i bråkform hela vägen. Då går det att göra helt och hållet i huvudet (det är ju inte så lätt att veta att annars). Då ser det ut så här:




