’Förenkla uttryck’ - varför gör jag såhär och lyckas inte rationalisera mig fram?
Hej
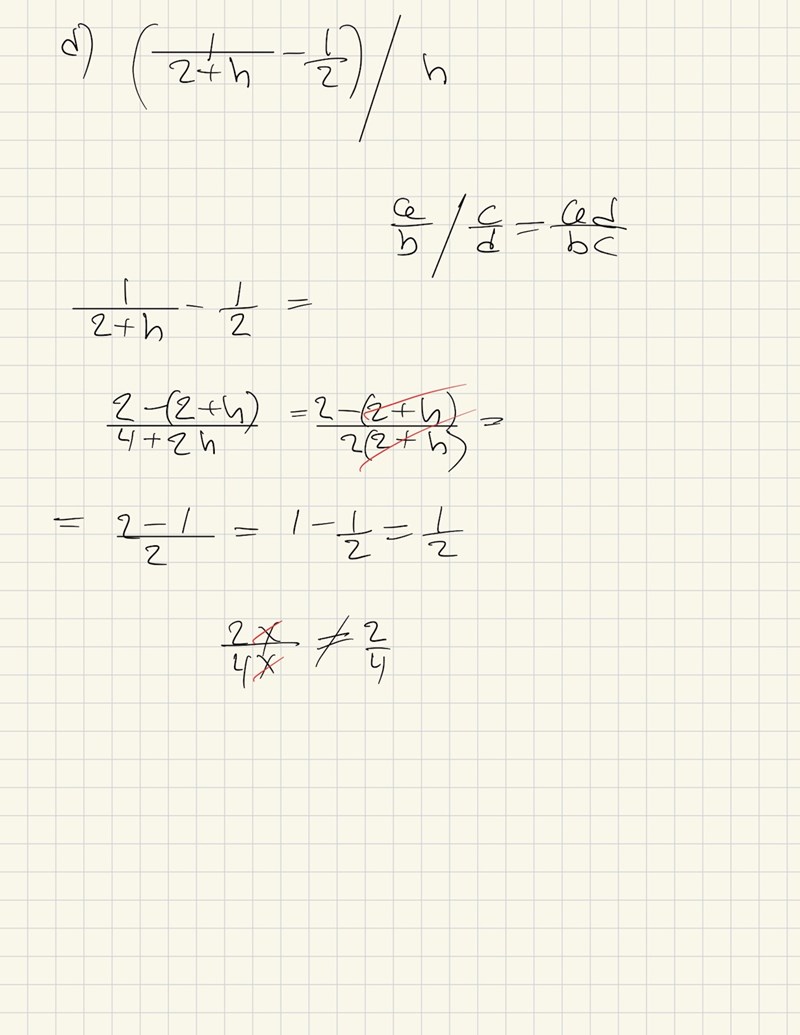
är jag hjärndöd?
mvh
Kan du motivera vad det är för matematisk operation du gör när du stryker 2+h? Det stämmer nämligen inte.
Laguna skrev:Kan du motivera vad det är för matematisk operation du gör när du stryker 2+h? Det stämmer nämligen inte.
Det heter att jag förkortar.:)
maratmatorkin skrev:Det heter att jag förkortar.:)
Problem är att förkortning inte fungerar så här.
Det är endast gemensamma faktorer som kan förkortas. Finns det flera termer i täljaren och/eller nämnaren och om man vill förkorta någonting, så behöver man först bryta ut gemensamma faktorer som därefter kan strykas.
När du skriver så är (2+h) i täljaren inte en utbruten faktor, så den får inte strykas.
Man kan lätt kontrollera att genom att sätta in något enkelt värde på .
T.ex. ger .
När du kommit fram till , så behöver du förenkla täljaren först, så det blir i täljaren.
LuMa07 skrev:maratmatorkin skrev:Det heter att jag förkortar.:)
Problem är att förkortning inte fungerar så här.
Det är endast gemensamma faktorer som kan förkortas. Finns det flera termer i täljaren och/eller nämnaren och om man vill förkorta någonting, så behöver man först bryta ut gemensamma faktorer som därefter kan strykas.
När du skriver så är (2+h) i täljaren inte en utbruten faktor, så den får inte strykas.
Man kan lätt kontrollera att genom att sätta in något enkelt värde på .
T.ex. ger .
När du kommit fram till , så behöver du förenkla täljaren först, så det blir i täljaren.
Tack för en mer formell förklaring. Jag gillar formalitet. :3
då ser jag det bättre. Tyckte bara att jag hade faktorn -1 i täljaren men jag köper din förklaring. Tack!



