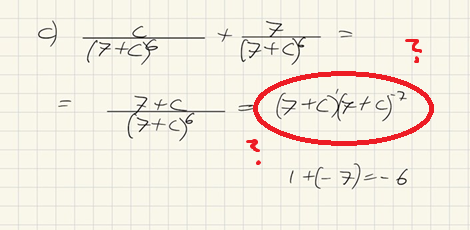”Förenkla uttrycken”. Har jag uttryckt potensen rätt?
Hej.
fick en liten brainfjärt eller vad man ska säga.
är det här rätt uttryckt när man omvandlar till multiplikation? Alltså att ena binomet är upphöjt till ett och då får man subtrahera potensen med ett i andra binomet?
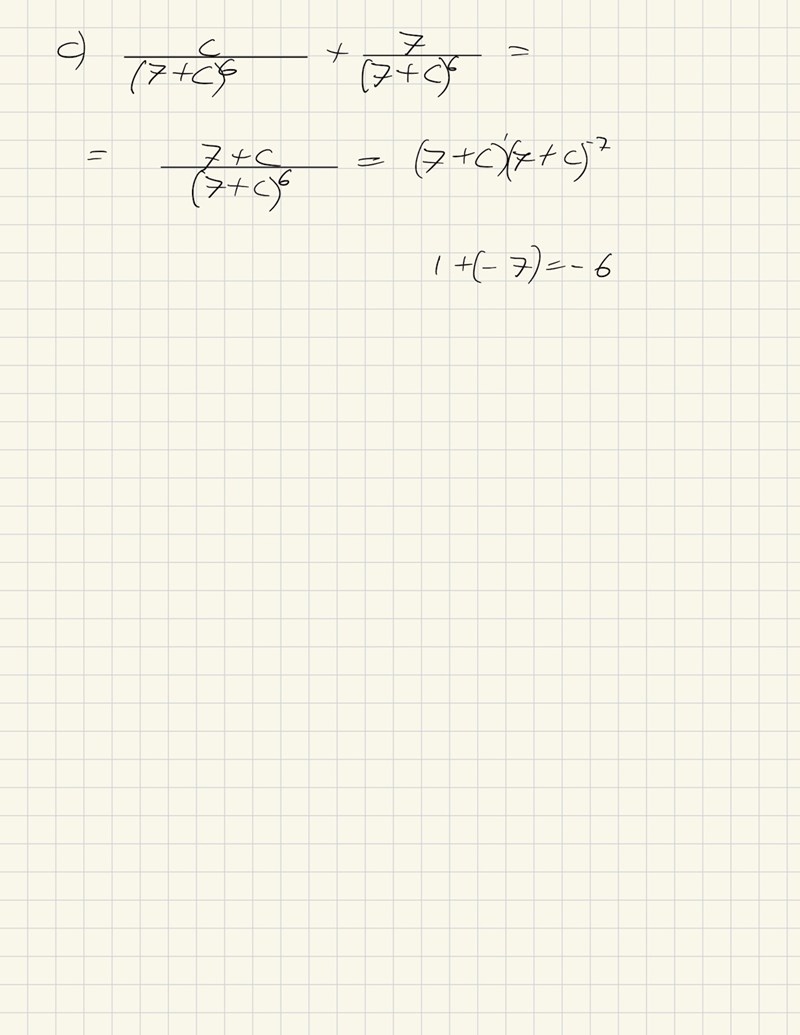
Mvh
Jag hänger med ända hit. Sedan händer märkliga saker.
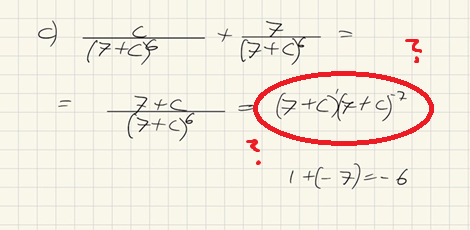
Du kan absolut lyfta upp nämnaren, men det ger inte -7 i exponenten:
Detta kan du skriva om till om du vill.
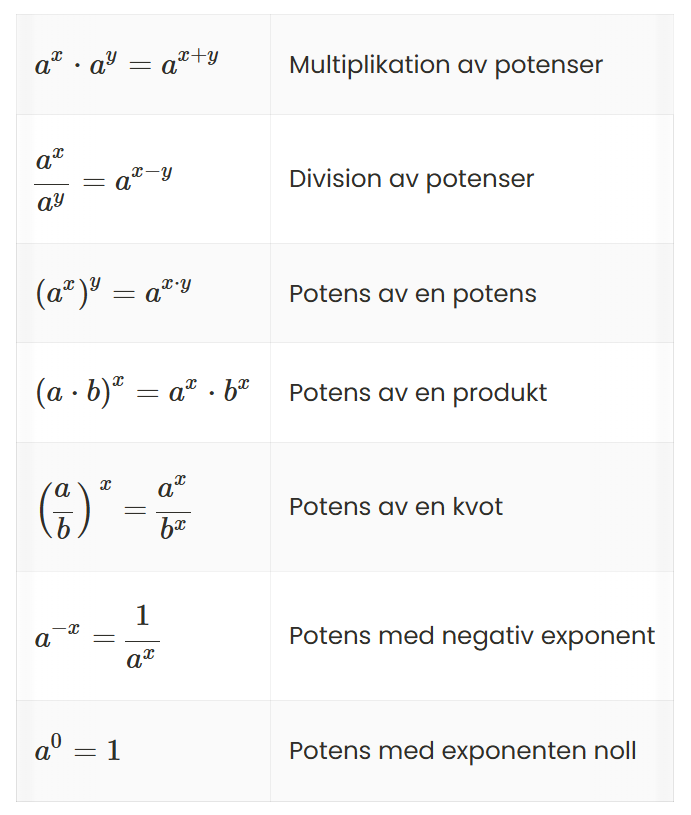
Generellt gäller:
sictransit skrev:Jag hänger med ända hit. Sedan händer märkliga saker.
Du kan absolut lyfta upp nämnaren, men det ger inte -7 i exponenten:
Detta kan du skriva om till om du vill.
Generellt gäller:
Ja just det ja! En försvinner ju i nämnaren för att göra uttrycket lika med 1 och resterande 5 anger potensens grad. Varit sjuk i en vecka och mycket som spökar i huvudet gällande grundläggande matematik😬. Tack för det sista uttrycket som generell regel. Det hjälper oerhört att kunna memorera som det står i exempelvis formelblad och kunna referera till mentalt när det känns osäkert. Tack!
maratmatorkin skrev:Ja just det ja! En försvinner ju i nämnaren för att göra uttrycket lika med 1 och resterande 5 anger potensens grad. Varit sjuk i en vecka och mycket som spökar i huvudet gällande grundläggande matematik😬. Tack för det sista uttrycket som generell regel. Det hjälper oerhört att kunna memorera som det står i exempelvis formelblad och kunna referera till mentalt när det känns osäkert. Tack!
Bra att det klarnade!
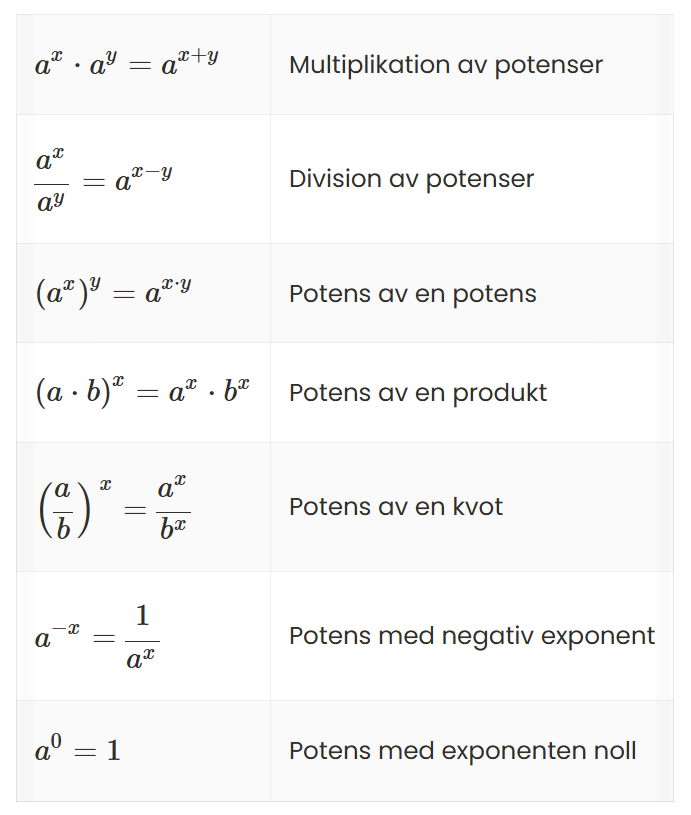
Potenslagarna (och de snarlika logaritmlagarna) behöver man kunna utantill. De är inte så många.
Utan dem i bakhuvudet så blir mycket inom matten klurigt.
Är man osäker kan man alltid prova med små tal:
Ahh! Så var det ju:
sictransit skrev:maratmatorkin skrev:Ja just det ja! En försvinner ju i nämnaren för att göra uttrycket lika med 1 och resterande 5 anger potensens grad. Varit sjuk i en vecka och mycket som spökar i huvudet gällande grundläggande matematik😬. Tack för det sista uttrycket som generell regel. Det hjälper oerhört att kunna memorera som det står i exempelvis formelblad och kunna referera till mentalt när det känns osäkert. Tack!
Bra att det klarnade!
Potenslagarna (och de snarlika logaritmlagarna) behöver man kunna utantill. De är inte så många.
Utan dem i bakhuvudet så blir mycket inom matten klurigt.
Är man osäker kan man alltid prova med små tal:
Ahh! Så var det ju:
Tack!