Förenkla uttrycket
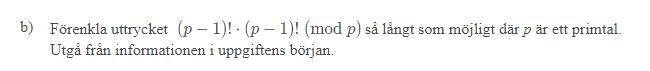
Jag har ingen anning hur jag kan börja. Det ända jag har kommit fram till är att:
Tack på förhand!
Lite utanför mitt kunskapsområde. Man skall nyttja något som heter Wilson's theorem(se wikipedia), n primtal 
Det följer dock inte anvisad metod.
rapidos skrev:Lite utanför mitt kunskapsområde. Man skall nyttja något som heter Wilson's theorem(se wikipedia), n primtal
Det följer dock inte anvisad metod.
Facit:
Jag har aldrig hört talas om någon Wilson's theorem, men jag hittade facit. Tyvärr förstår jag inte alls vad de har gjort dock.
Enligt satsen: Varje tal 1,2,3,...,p-1 har en invers. Antingen talet själv eller ett annat tal.
Antag att talet har sig själv som invers, dvs x2 = 1(mod p).
=> x2 = k*p + 1 => x =1 eller så antar vi att x = p - y => p2 -2yp + y2 = k*p + 1 => y = 1
Alltså är x =1 (mod p) eller x = (p-1) (mod p)
=> (p-1)!(mod p)=1*2*3*4*...*(p-1)(mod p) =
/Alla tal 2,3,4,...,p-2 har en invers bland 2,3,4,...,p-2/ = (p-1)(mod p)
=> (p-1)!(p-1)! (mod p) = (p-1)2 (mod p) = p2 -2p + 1(mod p) = 1 (mod p)
Vet inte om det blev klarare. Talteori är svårt.
henrikus skrev:
/Alla tal 2,3,4,...,p-2 har en invers bland 2,3,4,...,p-2/ = (p-1)(mod p)
Tack för hjälpen
jag förstår att alla talen har en invers i det intervall, men jag förstår inte riktigt hur du, med den kunskapen, kom fram till (p-1)(mod p)
Skulle du kunna förklara det?
Tack på förhand!
