Förenkla uttrycket

Jag tänkte nånting såhär

I sjätte steget, hur får du fram en cos²(x) i täljaren. cos(x)-cos(x) bör ju ta ut varandra och då får man kvar 2*cos(x)*sin(x). Utöver det är det rätt att använda konjugat så bra jobbat.

vimärbäst skrev:

I sjätte steget, hur får du fram en cos²(x) i täljaren. cos(x)-cos(x) bör ju ta ut varandra och då får man kvar 2*cos(x)*sin(x)

Menar du här ?

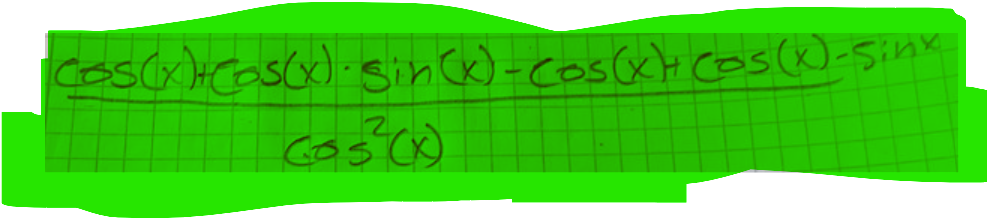
Ja, +cos(x) och -cos(x) bör ta ut varandra och cos(x)sin(x)+cos(x)sin(x) bör du förenkla till 2cos(x)sin(x).

 Tack !Jag gör ett nytt försök

vimärbäst skrev:

Ja, +cos(x) och -cos(x) bör ta ut varandra och cos(x)sin(x)+cos(x)sin(x) bör du förenkla till 2cos(x)sin(x).

bryter du ut $\sin \left(x\right)\hspace{0.17em}?$

Nej men jag förenklar utrycket för att då $\pm$cos(x) tar ut varandra så har vi kvar cos(x)*sin(x)+cos(x)*sin(x) som jag förenklar till 2*cos(x)*sin(x).

varför tar cosx och -cos x utvarandra. De multipliceras med sinx ?

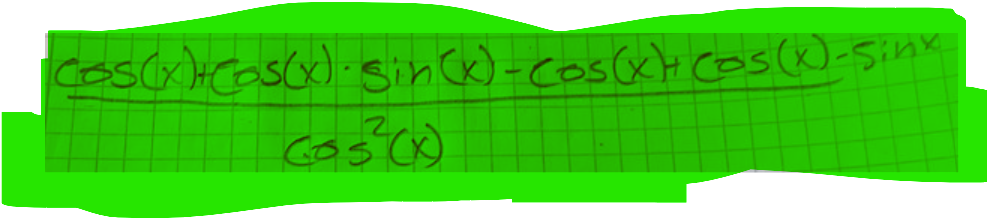
om du kollar på bilden har vi först i täljaren en cos(x)+cos(x)sin(x)-cos(x)+cos(x)sin(x) eftersom det är plus och minus tar cos(x)-cos(x) ut varandra

tar också -cos(x)+cos(x) utvarandra på Hl ?

Högerled är ju bara 2*tan(x), så vad menar du?

jag får det till

Tillägg: 31 aug 2025 12:23

$\frac{-{\sin }^2\left(x\right)}{{\cos }^2\left(x\right)}$

Tack! Jag ska kika närmare.

Det här är min lösning;

Bra jobbat!