Förenkla uttrycket
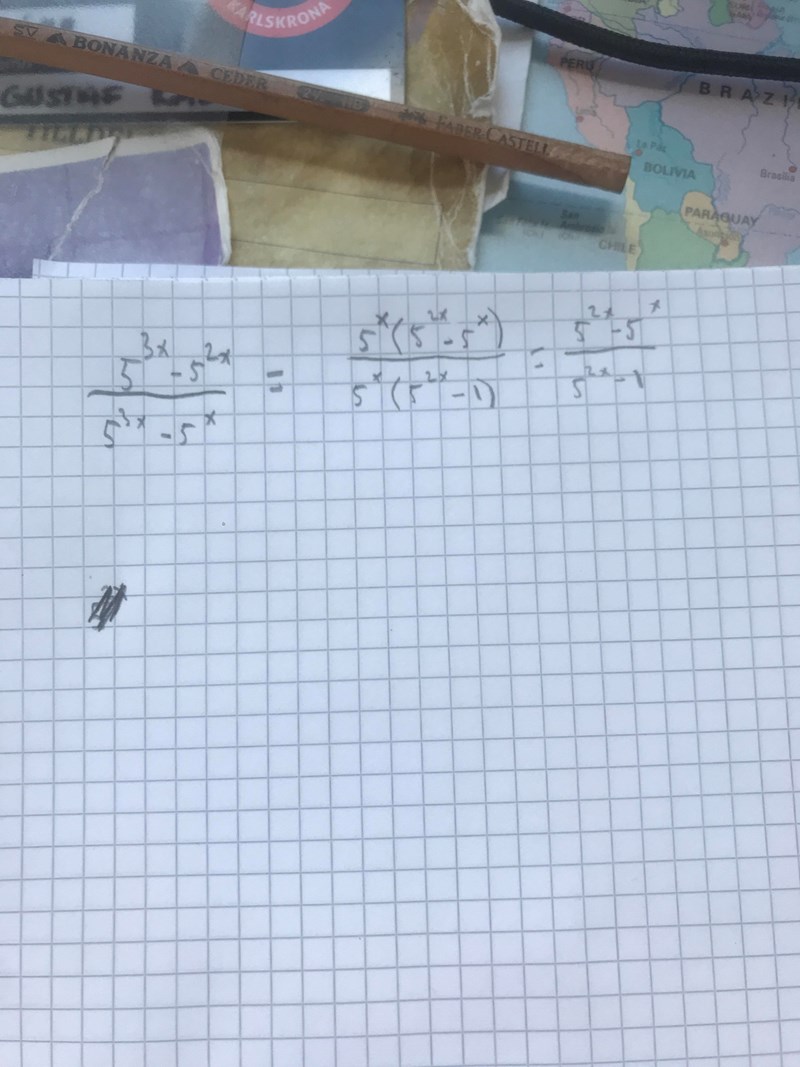
Förenkla följandd uttryck: (5^3x-5^2x)/(5^3x-5^x) Jag kommer bara så pass långt som på bilden, men man ska kunna komma ännu längre. Vad är nästa steg?
Du kan bryta ut från täljaren, och vad det gäller nämnaren: Kom ihåg att . Finns det någon känd regel du skulle kunna använda för att faktorisera ?
Du kan bryra ut en gememsam faktor i täljaren. Nämneren är ett tal i kvadrat minus ett annant tal i kvadrat. Vilken regel kan du använda då? Sedan ser du nog själv vad du kan göra.
Smutstvätt skrev:Du kan bryta ut från täljaren, och vad det gäller nämnaren: Kom ihåg att . Finns det någon känd regel du skulle kunna använda för att faktorisera ?
Konjugat är den du tänker på va? Men roten ur 5 blir ju inte jämnt direkt...
Smaragdalena skrev:Du kan bryra ut en faktor 5x i täljaren. Du kan använda konjugatregeln på nämneren. Sedan ser du nog själv vad du kan göra.
Gjorde så här. Svaret blev nu rätt. Tack för hjälpen.

Nej, roten ur 5 är inte särskilt jämnt, men roten ur 52x är.



