Förenkling av divisioner med -1 utbrytning.

Freemind skrev:

...
Så ena uppgiften är (b-a/a-b)^2. Så jag skrev ut det såhär: (b+a)(b-a) / (a+b)(a-b). På så vis kunde jag enkelt stryka b+a och a+b för dom är likadana. Men a-b och b-a är inte det. 
Då gjorde jag så att jag ändra täljaren. (-1)(a-b) / a-b . På så vis är täljaren likadan men byt plats på dem. Om jag följer andra tal jag gjort sedan tidigare så borde svaret bli -1 ? 
Gjorde en liknande där det var 8-x / x-8 och då gjorde jag likadant, bröt ur -1 och tog x-8/x-8 och hade en -1 kvar. Men facit säger att svaret är 1. Så jag vet inte hur dom gjort där. 

...

Du tänker rätt med att bryta ut -1 ur täljaren, men du glömmer kvadreringen på slutet.

Eftersom (b-a) = -1*(a-b) så gäller att (b-a)/(a-b) = -1*(a-b)/(a-b) = -1 och alltså är ((b-a)/(a-b))^2 = (-1)^2 = 1.

(Detta gäller såklart under förutsättningen att a är skilt från b. Annars är uttrycket odefinierat.)

Gör en ny tråd för den andra uppgiften.

-------------

Och kom ihåg att skriva ut ordentligt med parenteser så att uttrycken blir rätt.

$\frac{b-a}{a-b}$ skrivs som (b-a)/(a-b), inte som b-a/a-b.

Ja självklart. Eftersom jag skrev in -1 efter jag kvadrerat. Tack. 

Det är väldigt svårt att hänga med i det du skriver, eftersomdu slarvar så förfärligt med parenteserna.

Till att börja med skriver du (b-a/a-b)². Så som du har skrivit det betyder det $(b-\frac{a}{a}-b)^2=(b-1-b)^2=1^2=1$, men jag gissar av det du skriver senare att du egentligen menar ((b-a)/(a-b))²=(-(a-b)/(a-b))²=(-1)²=1.

På andra uppgiften skriver du a²-1/a-a²=-1/a men jag gissar att du menar $(a^2-1)/(a-a^2)$. Du kan inte "stryka" termer på det sättet, det är bara faktorer som kan förkortas. Se till att faktorisera täljare och nämnare, så kan du förkorta bort en faktor.

Vill bara säga att jag löste andra uppgiften. Gick tillbaks och förstod var felet var. Så behöver inte hjälp med den.
Löste det med a^2-1 / -a(a-1) , då blev det a+1 / -a som i facit. 

Freemind skrev:

Vill bara säga att jag löste andra uppgiften. Gick tillbaks och förstod var felet var. Så behöver inte hjälp med den.
Löste det med a^2-1 / -a(a-1) , då blev det a+1 / -a som i facit. 

 Slarva inte med parenteser.

$\frac{a^2-1}{-a(a-1)}$ skrivs som (a^2-1)/(-a(a-1)), inte som a^2-1 / -a(a-1).

Ser du skillnaden?

Smaragdalena skrev:

Det är väldigt svårt att hänga med i det du skriver, eftersomdu slarvar så förfärligt med parenteserna.

Till att börja med skriver du (b-a/a-b)². Så som du har skrivit det betyder det $(b-\frac{a}{a}-b)^2=(b-1-b)^2=1^2=1$, men jag gissar av det du skriver senare att du egentligen menar ((b-a)/(a-b))²=(-(a-b)/(a-b))²=(-1)²=1.

På andra uppgiften skriver du a²-1/a-a²=-1/a men jag gissar att du menar $(a^2-1)/(a-a^2)$. Du kan inte "stryka" termer på det sättet, det är bara faktorer som kan förkortas. Se till att faktorisera täljare och nämnare, så kan du förkorta bort en faktor.

(b-a/a-b)^2 skrivs i boken. Facit säger att det går att förenkla det till (b-a)^2 / (a-b)^2. 

Aah, det gör jag. Skrev allt snabbt bara så det blev att jag gjorde det enkelt för mig. Och då blev det slarv. 

När jag tittar på det igen, så kanske det inte ska skrivas på det viset. Men på det sättet som det ser ut i boken så är det b-a/a-b och 2 parenteser som täcker hela uträkningen och ^2 utanför. 

När jag tittar på det igen, så kanske det inte ska skrivas på det viset. Men på det sättet som det ser ut i boken så är det b-a/a-b och 2 parenteser som täcker hela uträkningen och ^2 utanför.

Är du säker på att det inte är skrivet med ett långt bråkstreck?

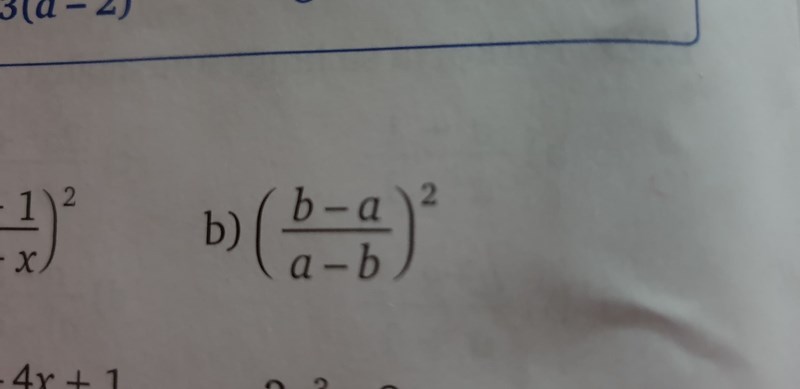Vet inte hur jag ska förklara det bättre än "b-a/a-b och 2 parenteser som täcker hela uträkningen med ^2 utanför." 
Men när vi inte kan skriva på det här viset, så är det nog som du säger. Att det skrivs ((b-a) / (a-b))^2. 

Grejen är att i boken så skrivs det aldrig med parenteser som ni gör. Tex står det "5-2 / 4-1" så skriver inte dom i boken (5-2) / (4-1)

Så när jag skriver till er, så säger ni att jag slarvar med parenteser, vilket är rätt. Men jag kopierar hur boken skrivit det. Därav förvirringen.

Freemind skrev:

Vet inte hur jag ska förklara det bättre än "b-a/a-b och 2 parenteser som täcker hela uträkningen med ^2 utanför." 
Men när vi inte kan skriva på det här viset, så är det nog som du säger. Att det skrivs ((b-a) / (a-b))^2. 

Grejen är att i boken så skrivs det aldrig med parenteser som ni gör. Tex står det "5-2 / 4-1" så skriver inte dom i boken (5-2) / (4-1)

Så när jag skriver till er, så säger ni att jag slarvar med parenteser, vilket är rätt. Men jag kopierar hur boken skrivit det. Därav förvirringen.

 Nej, det är inte korrekt att påstå att du "kopierar hur boken har skrivit". Tycker du att "$(\frac{b-a}{a-b})^2$" och "(b-a/a-b)^2" ser ut som kopior av varandra? Din bok använder sig av ett långt bråkstreck, vilket betyder att det finns en "inbyggd" parentes runt täljaren och en runt nämnaren. När du skriver uttrycket med snett bråkstreck "/" måste du sätta dit parenteserna själv.

Ja jag tyckte dom var likadana. Annars hade jag aldrig använt mig av dem på det viset. Jag har aldrig fått förklarat för mig att det finns en inbyggd parentes med långt bråkstreck och inte när man använde sig av "/". För alla webbsidor har inte eran funktion att kunna skriva bråktecken. Så jag trodde då att "aha på datorn då, så är / = bråkstrecket, och inte att / = bråkstreck utan parenteser. När jag gick i skolan och pluggade matte så använde vi inte datorn direkt. Detta är första gången jag skrivit med datorn, då jag pluggar distans.