förenkling av ett uttryck

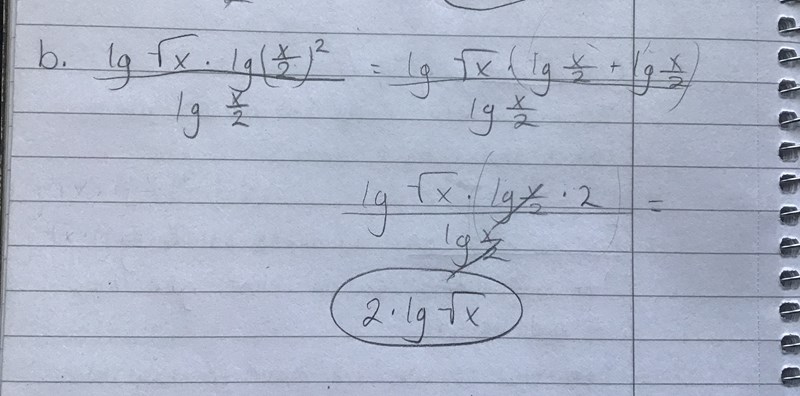
När man håller på med logaritmer så betecknar exponenter vid parentesen att det är själva logaritm-talet som är multiplicerar med sig självt. Inte argumentet 

Dvs att

$\lg(a)^2 = (lg(a))^2 = \lg(a) \cdot \lg(a)$

är ekvivalenta uttryck och att

$\lg(a)^2 \neq \lg(a^2) = 2 \lg(a) = \lg(a) + \lg(a)$

Därmed så gäller det inte att 

$\lg(\frac{x}{2})^2 = \lg(\frac{x}{2}) + \lg(\frac{x}{2})$

utan istället gäller att

$\lg(\frac{x}{2})^2 = \lg(\frac{x}{2}) \cdot \lg(\frac{x}{2})$

Skriv om $\sqrt x$ till $\lg x^{\frac{1}{2}}$och använd en logaritmlag.

Jag kommer inte längre än såhär :/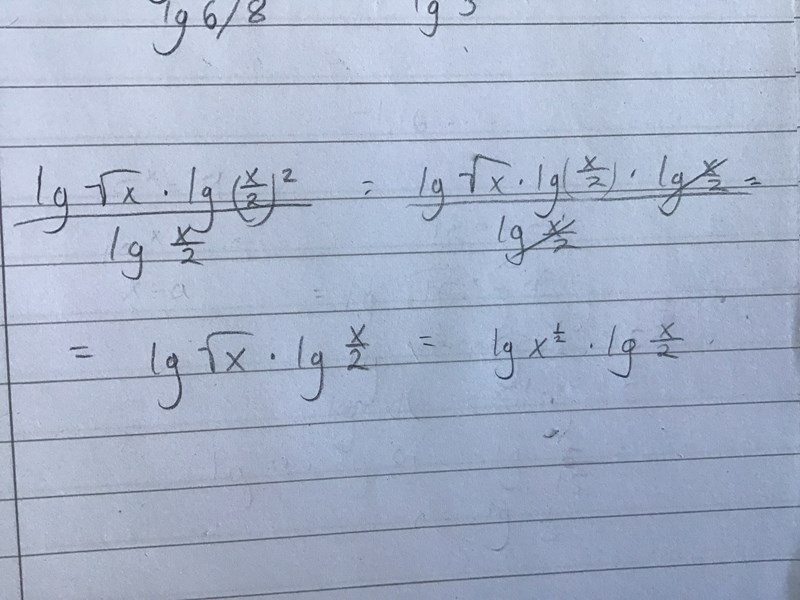

SeriousCephalopod skrev:

När man håller på med logaritmer så betecknar exponenter vid parentesen att det är själva logaritm-talet som är multiplicerar med sig självt. Inte argumentet 

Dvs att

$\lg(a)^2 = (lg(a))^2 = \lg(a) \cdot \lg(a)$

är ekvivalenta uttryck och att

$\lg(a)^2 \neq \lg(a^2) = 2 \lg(a) = \lg(a) + \lg(a)$

Därmed så gäller det inte att 

$\lg(\frac{x}{2})^2 = \lg(\frac{x}{2}) + \lg(\frac{x}{2})$

utan istället gäller att

$\lg(\frac{x}{2})^2 = \lg(\frac{x}{2}) \cdot \lg(\frac{x}{2})$

Jag vill inte säga något kategoriskt om notationen, men det ser ut som om trådskaparen gjorde rätt tolkning och fick fram rätt svar, bara en smula oförenklat. Med Smaragdalenas tips gör man färdigt förenklingen. 

$lg\sqrt{x } · lg{\left(\frac{x}{2}\right)}^2÷ lg\left(\frac{x}{2}\right)$

$$\begin{gathered} \frac{{\displaystyle lg{x}^{1/2}·lg(\frac{{\displaystyle x}}{{\displaystyle 2}}{)}^2}}{{\displaystyle lg\frac{{\displaystyle x}}{{\displaystyle 2}}}} \\ \frac{{\displaystyle lg{x}^{1/2}·2lg\left(\frac{{\displaystyle x}}{{\displaystyle 2}}\right)}}{{\displaystyle lg\frac{{\displaystyle x}}{{\displaystyle 2}}}} \\ lg{x}^{1/2} ·2 = lgx \end{gathered}$$