Förenkling av indexräkning

Jag ser åtminstone två fel. 

Tänk på att $\varepsilon_{ijk}\varepsilon_{jlm}=-\varepsilon_{jik}\varepsilon_{jlm}$

Det är också viktigt att notera att deriveringsoperatorn bara verkar på $r_k$ i uttrycket. Den ska inte derivera $A$

D4NIEL skrev:

Jag ser åtminstone två fel. 

Tänk på att $\varepsilon_{ijk}\varepsilon_{jlm}=-\varepsilon_{jik}\varepsilon_{jlm}$

Det är också viktigt att notera att deriveringsoperatorn bara verkar på $r_k$ i uttrycket. Den ska inte derivera $A$

Jag förstår inte dina markeringar och pilar. Vad är felet med eijkejlm om vi börjar där? Varför är det bättre att omvandla eijk=-ejik för att använda sambandet med kroneckerdelta? En annan sak också är att vi har di(Akrk) och du säger att Ak inte ska deriveras, men i frågan säger de att A är ett deriverbart fält, varför kan man inte använda produktregeln för att derivera båda Ak och rk?

Indexet du kontraherar över måste stå på samma plats. I den första faktorn står $j$ på plats $2$, i den andra faktorn står $j$ på plats $1$. Byt plats på indexen så att de matchar formelsamlingens formel för Levi-Civita symbolens kontraktion. 

Såhär fick jag för att matcha sambandet för eijkeklm. Men detta ger mig 0 som svar vilket är konstigt.

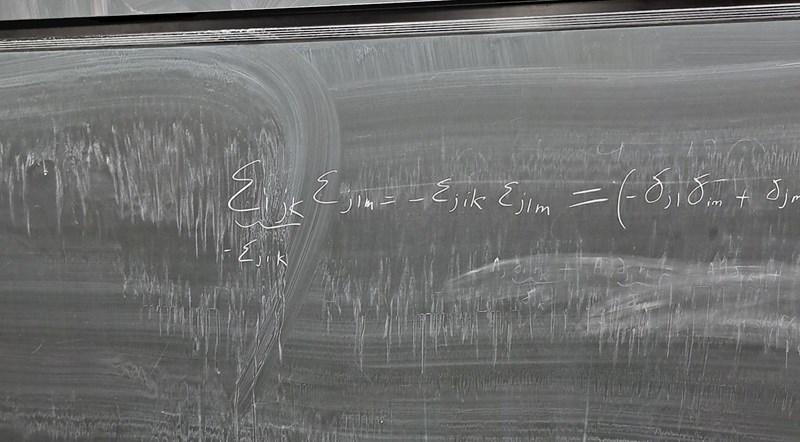
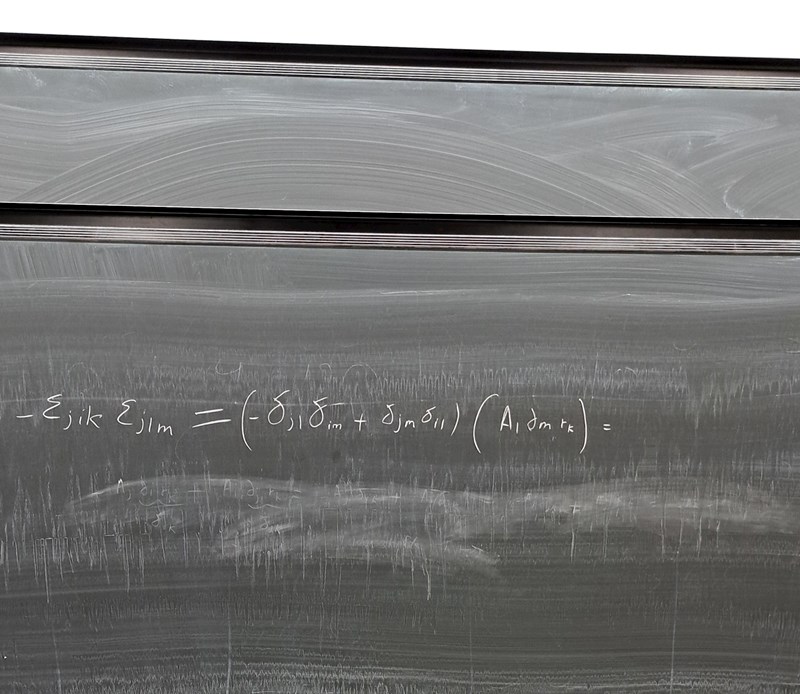
Men nu har du ju fått med $j$ som index trots att det är det index vi summerar över (som alltså ska kontraheras bort)

$\varepsilon_{ijk}\varepsilon_{jlm}=-\varepsilon_{jik}\varepsilon_{jlm}=-(\delta_{il}\delta_{km}-\delta_{im}\delta_{kl})=(\delta_{im}\delta_{kl}-\delta_{il}\delta_{km})$

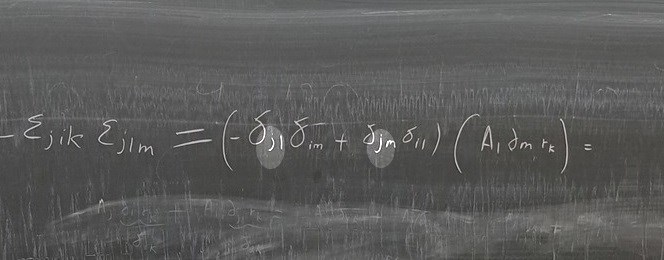
Dubbelkolla med formelsamlingen om du inte kan kontraktionen av två Levi-Civita utantill.

D4NIEL skrev:

Men nu har du ju fått med $j$ som index trots att det är det index vi summerar över (som alltså ska kontraheras bort)

$\varepsilon_{ijk}\varepsilon_{jlm}=-\varepsilon_{jik}\varepsilon_{jlm}=-(\delta_{il}\delta_{km}-\delta_{im}\delta_{kl})=(\delta_{im}\delta_{kl}-\delta_{il}\delta_{km})$

Dubbelkolla med formelsamlingen om du inte kan kontraktionen av två Levi-Civita utantill.

Ja okej då förstår jag. Jo jag såg formelsamlingen nu och rättade till detta. Har äntligen löst uppgiften nu. Tack!