Förhållande mellan två trianglars areor
Hej!
Jag har problem med att lösa en uppgift 4246 b) . Jag har löst uppgiften med Pythagoras sats och har fått rätt svar som facit säger; 0,19. Grejen är den att man egentligen inte ska lösa uppgiften med den satsen eftersom läroboken inte nämnt satsen än. Jag vet dock inte hur man löser uppgiften utan den satsen. Skulle någon kunna hjälpa mig?
Edit: Tusan, jag läste slarvigt och löste a) uppgiften.
Du har två trianglar som är likformiga.
Den ena har hypotenusan 9 och "basen" 10 - x.
Den andra har hypotenusan 10 och basen 9.
Därför är den andra en uppskalad med en faktor av 10/9 gentemot den första. Så därför får man att skalar man upp basen i den första med faktorn 10/9 så ska man få längden på basen i den andra. Alltså
10/9 * (10 - x ) = 9
Denna har lösningen x = 19/10.
Kalla höjden i den största triangeln för h. Då kan du ställa upp uttryck för arean av den största och minsta triangeln som båda innehåller h.
När du sedan dividerar uttrycken med varandra kan du förkorta bort h.
Fråga igen om detta inte hjälper!
Jag fattar fortfarande inte. :( X vet jag är 1,9 från a-uppgiften. Och jag har ritat upp den största och den minsta triangeln, men jag vet inte hur jag ska kunna räkna arean utan Pythagoras sats.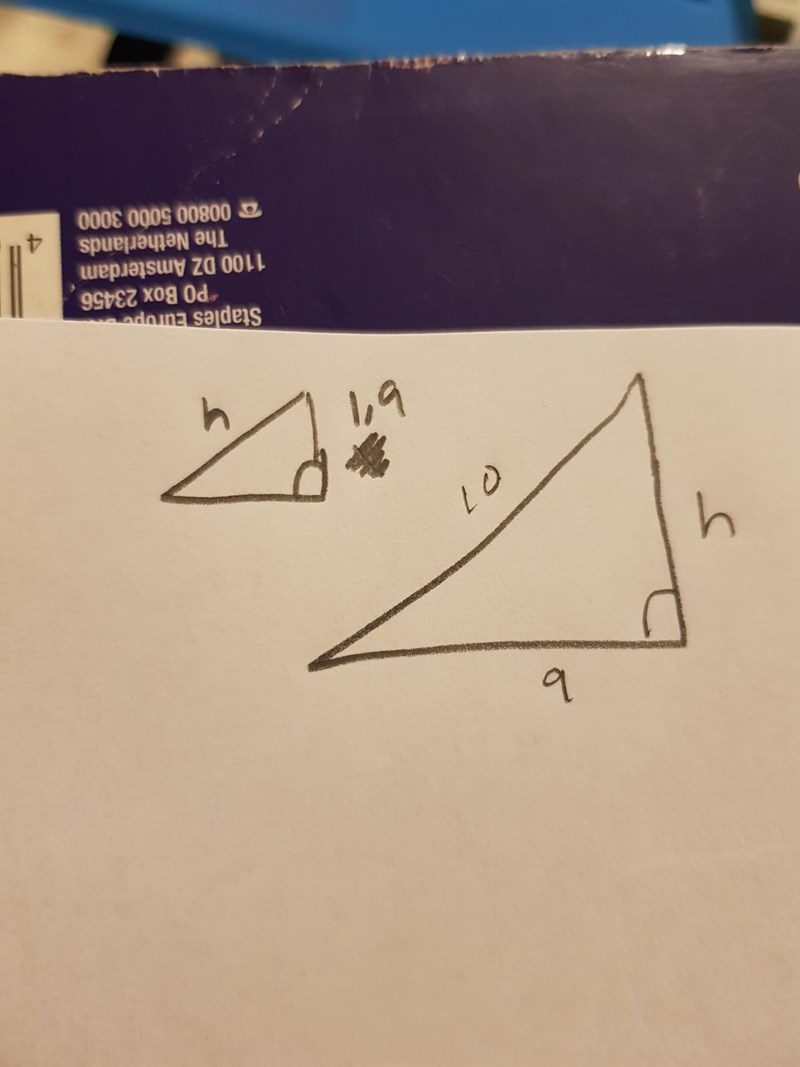
Den lilla triangeln har basen x och höjden h. Den största triangeln har höjden h och basen 10. Så kvoten mellan areorna är
Nu ska du bara förenkla detta.
revolten skrev :Jag fattar fortfarande inte. :( X vet jag är 1,9 från a-uppgiften. Och jag har ritat upp den största och den minsta triangeln, men jag vet inte hur jag ska kunna räkna arean utan Pythagoras sats.
Du har tyvärr ritat fel. Kolla bilden i uppgiften igen!
Den STÖRSTA triangeln har basen 10 och höjden h.
Den MINSTA triangeln har basen h.
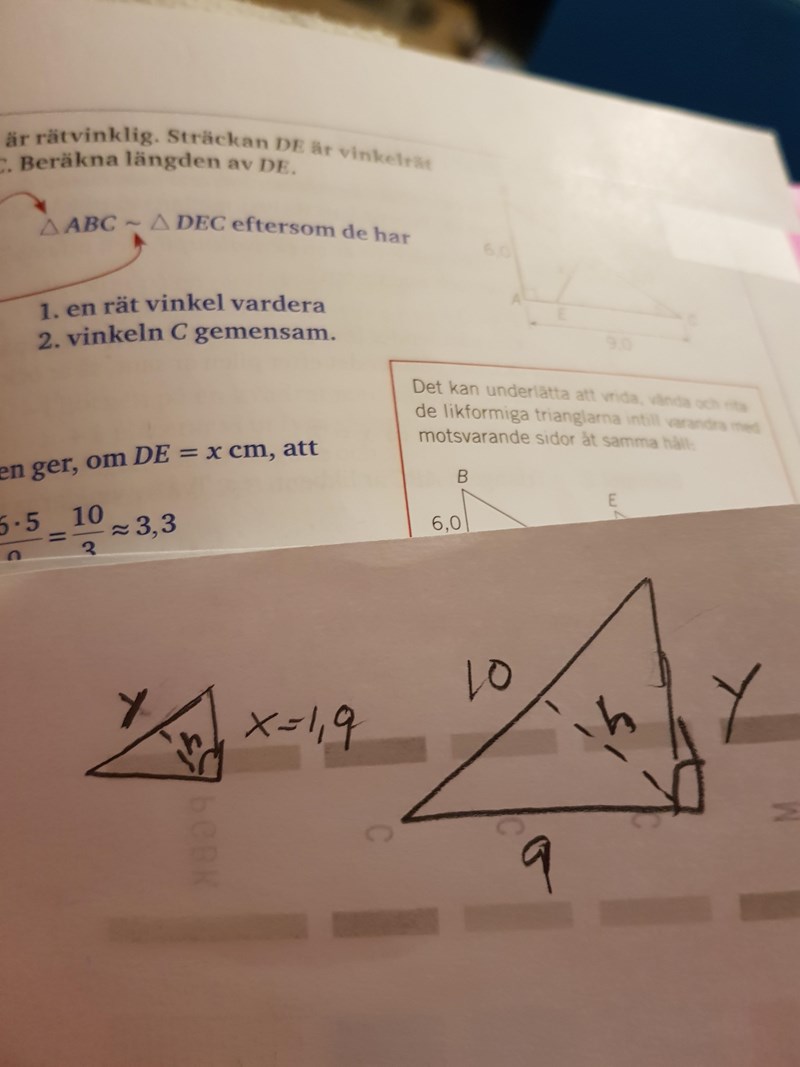Jag har ritat om trianglarna o bytt namn på sidan h till y men fattar fortfarande inte. Hur kan höjden på den lilla o den stora båda heta h? De är ju inte lika långa?
Jag förstod nu. Tack för hjälpen!
