Formel för antal vinklar
Hej
Hur får man fram en Formel enligt fråga 2213?
Klarade det inte så var tvungen att kolla Facit, så vet redan rätt svar. Undrar hur man skulle kunna göra för jag stirrar bara på svaret och har ingen aning om hur man ska komma fram till vet. Man ska väl se det bara men jag kan inte det.

Eftersom alla vinklar i en regelbunden -hörning är lika stora, blir målet att hitta vinkelsumman i en -hörning. Sedan är vinkelsumman/. Känns detta bra?
 Om man följer kanterna runt en n - hörning får man svänga 360/n grader vid varje hörn för att komma runt.
Om man följer kanterna runt en n - hörning får man svänga 360/n grader vid varje hörn för att komma runt.
Sen blir vinkeln i n-hörningen 180-360/n eller 180(1-2/n)
En annan variant: dra sträckor från alla hörn till mittpunkten. Då får man n trianglar. Hur stor är deras vinkel vid mittpunkten? Hur stor är summan av deras andra två vinklar då?
AlexMu skrev:Eftersom alla vinklar i en regelbunden -hörning är lika stora, blir målet att hitta vinkelsumman i en -hörning. Sedan är vinkelsumman/. Känns detta bra?
Ja, det låter rimligt.
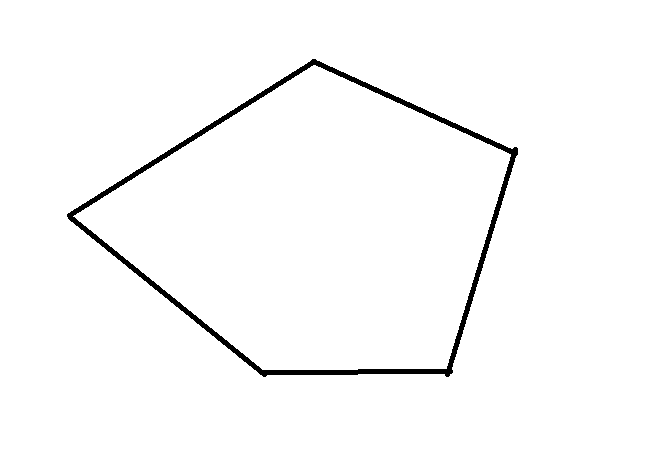
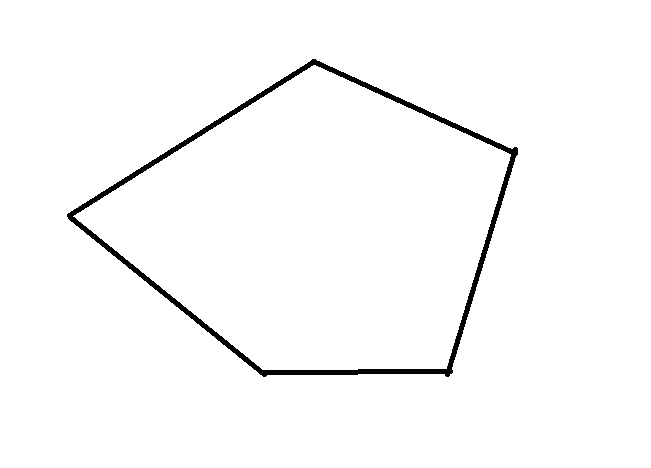
Tänk att vi har en -hörning (behöver inte vara regelbunden, i detta fall valde jag också en 5-hörning) som ser ut något såhär:
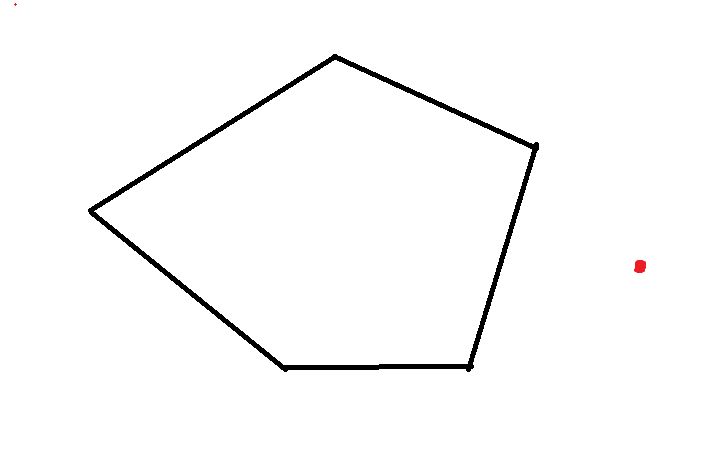
Vi tar och lägger till en punkt någonstans:
Och sedan drar lite linjer:

Slutligen, ta bort mittlinjen så får vi en hörning:
 Nu är frågan: Säg att vi känner till vinkelsumman i vår gamla -hörning, kalla den , hur många grader har vi "lagt till" till vår figur? Alltså utifrån och vår figur, vad blir ?
Nu är frågan: Säg att vi känner till vinkelsumman i vår gamla -hörning, kalla den , hur många grader har vi "lagt till" till vår figur? Alltså utifrån och vår figur, vad blir ?
AlexMu skrev:Tänk att vi har en -hörning (behöver inte vara regelbunden, i detta fall valde jag också en 5-hörning) som ser ut något såhär:
Vi tar och lägger till en punkt någonstans:
Och sedan drar lite linjer:
Slutligen, ta bort mittlinjen så får vi en hörning:
Nu är frågan: Säg att vi känner till vinkelsumman i vår gamla -hörning, kalla den , hur många grader har vi "lagt till" till vår figur? Alltså utifrån och vår figur, vad blir ?
Jag vet inte Alex. Beror inte det på vart vi sätter punkten.
Det bör det inte göra! Vinkelsumman i varje -hörning är alltid densamma. Så vilken vinkelsumma vi än lagt till måste den vara oberoende vart punkten är.
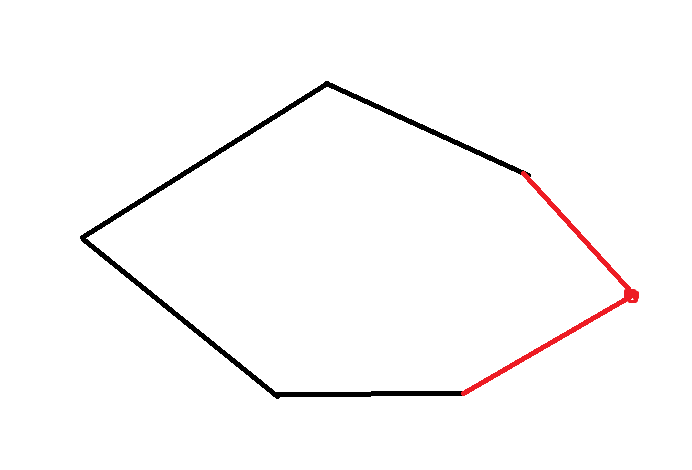
Det du kan tänka på är att vi egentligen sätter ihop två figurer: en -hörning och en triangel:
Okej.. då är den Vinkelsumman av Sn + 180 tänker jag..
Det stämmer! Det vi lägger till som vinkelsumma till -hörningen är de röda vinklarna i min bild, vilket alltid är 180 grader. Då vet vi att varje gång vi ökar antalet hörn med 1, så ökar vinkelsumman med 180 grader.
Vi kan se detta som exempel på en triangel och en fyrhörning. Triangel har 180 graders vinkelsumma medan fyrhörningen har 360 grader.
Kan du komma fram till den generella formeln utifrån detta?
Tyvärr, jag grejar det inte.
Så triangeln är 180, fyrhörning 360. Ökar med 180 per hörn.
Om 180 = n1
Men variabeln n står för hörn, och använder vi då en 3a där för triangeln så får vi alldeles för stort värde, så vi måste "backa" värdet för n kan man säga i och med att vi inte räknar ifrån n = 1. Medans man fortfarande subtraherar med n eftersom.. ja, det var hela uppgiften, så Vinkelsumman dividerat med antal hörn.. så
Så 180(n-2)/n