Formelfråga radieavstånd samt höjdavstånd
Sitter egentligen med ett programeringsproblem.
Söker efter en formel för att få fram höjden (med frågetecknet)
Jag har svaret till detta men undrar om det finns en formel till detta.
Vet att man kan räkna ut vinkeln först å ta det den vägen.
Problemet då är att det blir för mycket decimaler i maskinen som jag gör programmet till.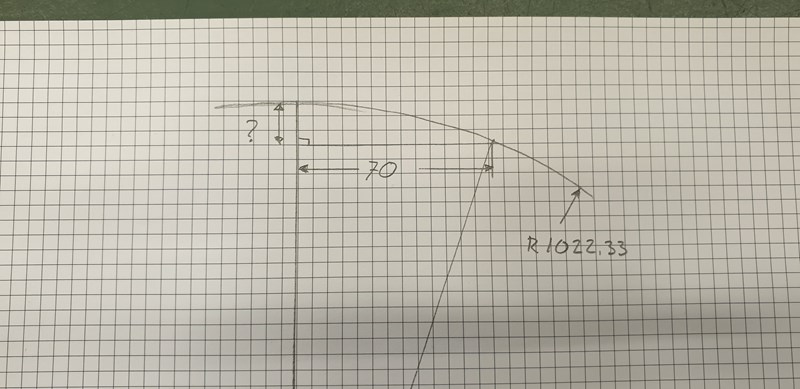
Tråd flyttad från Kluringar till Allmänna diskussioner. // Smutstvätt/Pepparkvarn, moderator
"För mycket decimaler i maskinen" låter intressant. Vad händer egentligen?
Du kan använda Pythagoras sats för att få avståndet från cirkelns centrum upp till den räta vinkeln.
Gogge skrev:Sitter egentligen med ett programeringsproblem.
Söker efter en formel för att få fram höjden (med frågetecknet)
Jag har svaret till detta men undrar om det finns en formel till detta.
Vet att man kan räkna ut vinkeln först å ta det den vägen.
Problemet då är att det blir för mycket decimaler i maskinen som jag gör programmet till.
Tråd flyttad från Kluringar till Allmänna diskussioner. // Smutstvätt/Pepparkvarn, moderator
Hej och välkommen till Pluggakuten!
EDIT - Lagunas metod är mycket enklare, jag tänkte inte på att det var en rätvinklig triangel vi har att göra med.
---------
Alternativ metod:
Kalla längden av sträckan som är utmärkt med ett frågetecken för x. Jag antar att denna sträcka är en del av cirkelns radie. Annars blir det svårt.
Denna sträcka är en del av en korda, nämligen cirkelns diameter.
Sträckan som är 70 lång är en halv korda.
Cirkelns diameter är 2*1022,33 = 2044,66 och delas i två delar: x och 2044,66 - x av den sistnämnda kordan.
Nu kan du sätta upp en ekvation för x med hjälp av kordasatsen.
Laguna skrev:"För mycket decimaler i maskinen" låter intressant. Vad händer egentligen?
Du kan använda Pythagoras sats för att få avståndet från cirkelns centrum upp till den räta vinkeln.
Det som händer med maskin är att den hanterar bara 8 siffror (oavsett heltal eller decimaltal)
Detta är bara ett exempel på hur problematiken kommer se ut.
Det är ett macro program till en virvelmaskin som jag sitter å klurar på.
Gogge skrev:Laguna skrev:"För mycket decimaler i maskinen" låter intressant. Vad händer egentligen?
Du kan använda Pythagoras sats för att få avståndet från cirkelns centrum upp till den räta vinkeln.
Det som händer med maskin är att den hanterar bara 8 siffror (oavsett heltal eller decimaltal)
Detta är bara ett exempel på hur problematiken kommer se ut.
Det är ett macro program till en virvelmaskin som jag sitter å klurar på.
Finns ens trigonometriska funktioner på maskinen? Har den kvadratrot?
8 siffror borde väl egentligen räcka till det här annars.
"Float" i många programspråk är inte mycket noggrannare.
Yngve skrev:Gogge skrev:Sitter egentligen med ett programeringsproblem.
Söker efter en formel för att få fram höjden (med frågetecknet)
Jag har svaret till detta men undrar om det finns en formel till detta.
Vet att man kan räkna ut vinkeln först å ta det den vägen.
Problemet då är att det blir för mycket decimaler i maskinen som jag gör programmet till.
Tråd flyttad från Kluringar till Allmänna diskussioner. // Smutstvätt/Pepparkvarn, moderator
Hej och välkommen till Pluggakuten!
EDIT - Lagunas metod är mycket enklare, jag tänkte inte på att det var en rätvinklig triangel vi har att göra med.
---------
Alternativ metod:
Kalla längden av sträckan som är utmärkt med ett frågetecken för x. Jag antar att denna sträcka är en del av cirkelns radie. Annars blir det svårt.
Denna sträcka är en del av en korda, nämligen cirkelns diameter.
Sträckan som är 70 lång är en halv korda.
Cirkelns diameter är 2*1022,33 = 2044,66 och delas i två delar: x och 2044,66 - x av den sistnämnda kordan.
Nu kan du sätta upp en ekvation för x med hjälp av kordasatsen.
Precis.. det blir båghöjden som efterfrågas i exemplet.
Kordan är väl a⋅b=c⋅d
Gogge skrev:
Precis.. det blir båghöjden som efterfrågas i exemplet.Kordan är väl a⋅b=c⋅d
Ja det är kordasatsen.
I vårt fall är , , och .
Det ger oss ekvationen
dvs
------
Lagunas metod med Pythagoras sats:
dvs
dvs
-----
Båda metoderna ger samma resultat, vilket är bra :-)
Nu har jag nog förklarat mej lite galet.. Det stämmer inte..
(Eller så är jag lite trög på morgonen)
Som sagt jag vet att svaret blir 2,399
Så efter en båge som löper neråt kan inte svaret bli 0.
Vet inte om bilden ger en tydligare förklaring.
Men visst att svaret blir lika är ju bara trevligt :-)

Gogge skrev:Nu har jag nog förklarat mej lite galet.. Det stämmer inte..
(Eller så är jag lite trög på morgonen)
Som sagt jag vet att svaret blir 2,399
Så efter en båge som löper neråt kan inte svaret bli 0.
Vet inte om bilden ger en tydligare förklaring.
Men visst att svaret blir lika är ju bara trevligt :-)
...
Din ursprungliga handritade bild visade en horisontell sträcka med längd 70 som ligger inuti cirkeln, dvs en del av en korda.
Den här bilden visar en sträcka som ligger utanför cirkeln, det verkar vara en del av en tangent.
Det är en helt annorlunda geometri och helt andra samband som gäller.
Jag förutsätter att de två linjerna utgår från cirkelns medelpunkt, dvs att de inte är parallella.
Då uppstår frågan vid vilken höjd som du har uppmätt avståndet 70 mellan de två linjerna. Är det vid punkt B eller C?

Om jag förklarar
Från punkt A "linje A" som vertikal linje
Från punkt B "linje B" son vertikal linje
Punk A & B är horisontell
70mm är alltså en parallell linje (A linje & B linje är alltså parallella)
Punkt C ligger i en radie (1022.33)
Centrum på radien ligger efter linje A
Mått 2,399 är, var radien skär i linje B
Gogge skrev:
Om jag förklarar
Från punkt A "linje A" som vertikal linje
Från punkt B "linje B" son vertikal linje
Punk A & B är horisontell
70mm är alltså en parallell linje (A linje & B linje är alltså parallella)
Punkt C ligger i en radie (1022.33)
Centrum på radien ligger efter linje A
Mått 2,399 är, var radien skär i linje B
Det där stämmer väldigt dåligt med din ursprungliga bild, där de båda linjerna definitivt inte är parallella:

Gogge skrev:Om jag förklarar
Från punkt A "linje A" som vertikal linje
Från punkt B "linje B" son vertikal linje
Punk A & B är horisontell
70mm är alltså en parallell linje (A linje & B linje är alltså parallella)
Punkt C ligger i en radie (1022.33)
Centrum på radien ligger efter linje A
Mått 2,399 är, var radien skär i linje B
OK om de två linjerna nerifrån och upp verkligen är parallella så stämmer det med din ursprungsbild och andragradsekvationen som jag formulerade stämmer eftersom avståndet 70 mellan de två linjerna då är lika stort inuti som utanför cirkeln.
Ekvationens lösning är .
Formeln är , där =radien, dvs .




