Försöker beräkna rotationsvolymen, varför blir det fel ?

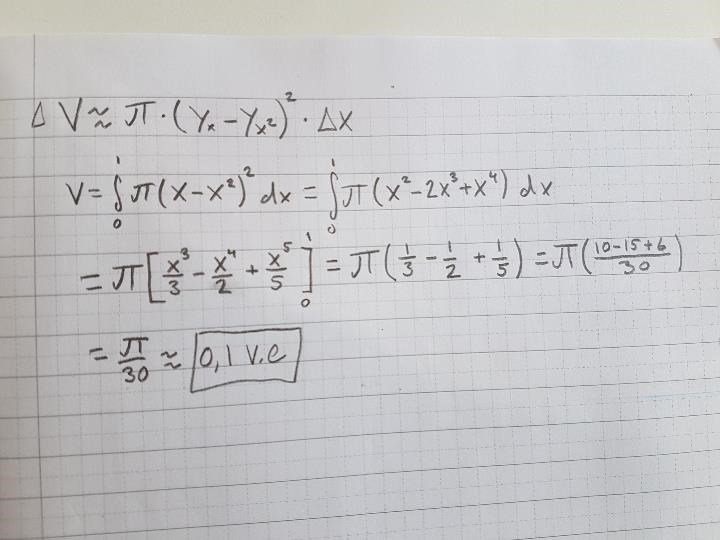
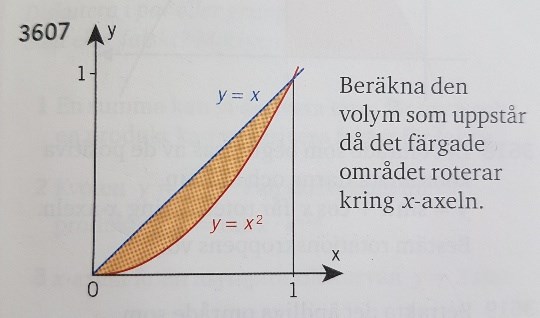
En vanlig skiva blir ju svår att använda. Kroppen kommer ha ett "hål" i mitten.

När du ställer upp dV hade den geometriskt rimligare versionen varit

$dV = \pi y_x^2 dx - \pi y_{x^2}^2 dx = \pi(y_x^2 - y_{x^2}^2)dx = \pi(x^2 - x^4)dx$

dvs volymen du får av att ta en större cirkelskiva och subtraherar bort en mindre cikrelskiva för att få arean av en annulus; cirkelskiva med ett cirkelformat hål i dess mitt. 

När du användt 

$dV = \pi(x - x^2)^2 dx$

så får dessa volymelement istället tolkas som volymen av en cirkelskiva vars radie är $x - x^2$ men detta skulle motsvara rotationsvolymen av en annan form än den aktuella, eller snarare att ci har cirkelskivor som är roterade runt (y = x)-linjen snarare än runt (y = 0)-linjen, dvs x-axeln, vilket är målet. 

Skillnaden blir en extra term i integralen som inte är korrekt när målet är att beräkna rotationsvolymn av det skuggade området. 

Ett trollinlägg bortplockad. /moderator

SeriousCephalopod skrev:

När du ställer upp dV hade den geometriskt rimligare versionen varit

$dV = \pi y_x^2 dx - \pi y_{x^2}^2 dx = \pi(y_x^2 - y_{x^2}^2)dx = \pi(x^2 - x^4)dx$

dvs volymen du får av att ta en större cirkelskiva och subtraherar bort en mindre cikrelskiva för att få arean av en annulus; cirkelskiva med ett cirkelformat hål i dess mitt. 

När du användt 

$dV = \pi(x - x^2)^2 dx$

så får dessa volymelement istället tolkas som volymen av en cirkelskiva vars radie är $x - x^2$ men detta skulle motsvara rotationsvolymen av en annan form än den aktuella, eller snarare att ci har cirkelskivor som är roterade runt (y = x)-linjen snarare än runt (y = 0)-linjen, dvs x-axeln, vilket är målet. 

Skillnaden blir en extra term i integralen som inte är korrekt när målet är att beräkna rotationsvolymn av det skuggade området. 

Bra förklarat, nu hänger jag med! tack!