Bygga grafisk förståelse för marginaltäthetsfunktionerna

Hejsan

Detta är min uppgift:

Vi fokuserar på a) och b).

När (X,Y) är likformigt fördelade över A antar $f_{X,Y}(x,y)$ det konstanta värdet $1/|A|$ pga, som jag förstått det, att över A är det lika stor sannolikhet att värdena hamnar i alla delytor förutsatt att de är lika stora samt att totala sannolikheten när $f_{X,Y}(x,y)$ integreras över området ska bli 1.

Men för att beräkna marginaltäthetsfunktionerna har jag svårt att visualisera. Det är enkelt att komma ihåg att man ska "integrera bort" den andra variabeln alltså

$f_X(x) = \int f_{X,Y}(x,y) dy$ ,

men vad är det som faktiskt händer här? Hur kan täthetsfunktionen för X ges av sannolikheterna map y på A? Jag försökt rita upp det men det gick inte så bra:

Det kanske är min bristande förståelse i flervarre men jag förstår inte heller varför man här kan räkna över hela området men för y måste det delas upp i $[-1,0]$ och $[0,1]$ ?

Följande intuition för diskreta slumpvariabler kanske kan vara till hjälp. Tänk att du har en slumpvariabel (X, Y) och X kan anta värdena 1 och 2 och Y kan anta värdena 1, 2, och 3. Vad är P(X = 1)? Det är en marginell sannolikhet och vi kan tänka på den som P(X = 1 och Y = 1) + P(X = 1 och Y = 2) + P(X = 1 och Y = 3).

Eftersom händelserna Y = 1, Y = 2 och Y = 3 utgör hela utfallsrummet för Y (och de inte överlappar) så kan sannolikheten för att X = 1 delas upp i fallen då Y = 1, 2, eller 3.

Vi har alltså uttryckt den marginella sannolikheten för X = 1 med den gemensamma sannolikhetsfördelningen för (X, Y).

Den generella formen skulle kunna skrivas

$P(X=x) = \sum_y P(X=x, Y=y),$

där vi summerar över alla y i utfallsrummet.

Det som händer i det kontinuerliga fallet är att vi istället för en summa får en integral:

$f_X(x) =P(X=x) =\int f_{X, Y}(x, y) dy,$

där vi integrerar över alla möjliga värden på Y. Tänk att en integral är som en kontinuerlig motsvarighet till en summa.

Angående visualisering så tycker jag denna bild från Wikipedia är bra:

Punkterna är värden från en bivariat normalfördelning, och vi kan tänka att de marginella fördelningarna är det vi får genom att "trycka ihop" den gemensamma fördelningen en dimension. Jag tror man kan tänka på det som en ortogonal projektion på ett plan. Här är en annan bild:

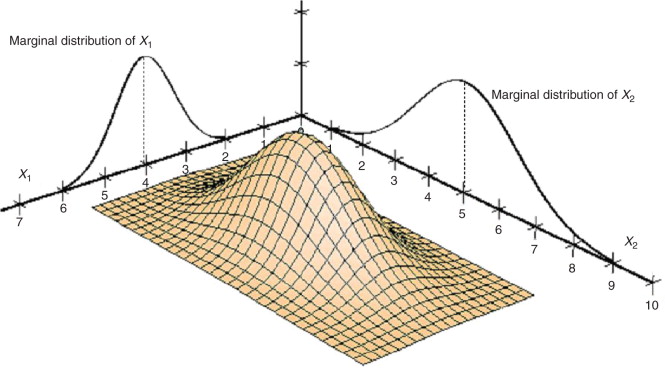Här får vi t.ex. den marginella fördelningen för X_1 genom att projicera den gemensamma fördelningen på planet X_2 = 0.

Källa: https://www.sciencedirect.com/topics/mathematics/marginal-distribution

Det var ju fantastiskt bra förklarat! Hade ju läst exakt det där men gjorde inte kopplingen själv.

Jag tror förresten att projektion inte är en korrekt intuition, utan det är bättre att tänka att man "trycker ihop" den gemensamma fördelningen till en platt pannkaka, som att fälla ihop ett teleskop. Finns det mer att trycka ihop på något visst ställe kommer den marginella fördelningen anta större värden där.

Om vi tar uppgiften i ditt inlägg och plattar ihop fördelningen--som vi tänker plottad på en z-axel: (x, y, f(x, y) )--till planet y = 0 (dvs vi omvandlar f(x, y) till den marginella fördelningen f(x) för X) så är en "slice" x = k från den gemensamma fördelningen f(x, y) större/har större area då k är nära 0 än när k är nära 1. Det gör att vi kommer få en marginell fördelning för X som antar större värden nära x = 0 än för x = 1, även fast vår ursprungliga fördelning f(x, y) har samma z-värde överallt. Så en projektion stämmer inte riktigt i detta fall.

Mycket riktigt så blir den marginella fördelningen något i stil med

$f_X(x) = c(\sqrt{1-x^2}+1)$ för $0\leq x\leq 1$ ,

som går från $f_X(0)=2c$ till $f_X(1)=c$ . Här är $c$ konstanten från den likformiga fördelningen $f(x, y) =c$ .

Det finns helt enkelt "mer" att göra pannkaka av när x är nära 0 än när x är nära 1 på grund av det cirkelbågsformade området, och eftersom vi har en likformig fördelning med samma höjd överallt.

För övrigt så behöver man när man ska ta fram $f_Y(y)$ dela upp integralen eftersom det för $-1\leq y\leq 0$ gäller att $0\leq x\leq 1$ , men för $0\leq y\leq 1$ gäller att $x\leq \sqrt{1-y^2}$ .

Ja, det sista förstod jag i efterhand. Jag var för dålig i envarre till och med.

Jag gjorde en liten bild, är inte säker på att jag beräknat de marginella tätheterna korrekt men:

Den vita kurvan är alltså $f_X(x)$ och den svarta är $f_Y(y)$ .

Svara

Visa senaste svar