Första ordningen differentialekvation

$$\begin{gathered} y\text{'}+e^{\sin x}y=e^{\sin x} \\ y\text{'}=e^{\sin x}-e^{\sin x}y \\ y\text{'}=(1-y)e^{\sin x} \\ \frac{1}{(1-y)}y\text{'}=e^{\sin x} 1-y\ne 0 \\ \frac{1}{(1-y)}dy=e^{\sin x}dx \\ \int \frac{1}{(1-y)}dy=\int e^{\sin x}dx \end{gathered}$$

Kan du fortsätta?

Kan du fortsätta?

Tror det...

blir det

$-\ln \left(\left|1-y\right|\right)+C=e^{\sin x}+C$

Men hur får man C, för att 

$$\begin{gathered} -\ln \left(\left|1-2\right|\right)=-\ln \left(1\right)=0 \\ {e}^{\sin \left(0\right)}=e^0=1 \\ C=1+C \end{gathered}$$

oneplusone2 skrev:

$$\begin{gathered} y\text{'}+e^{\sin x}y=e^{\sin x} \\ y\text{'}=e^{\sin x}-e^{\sin x}y \\ y\text{'}=(1-y)e^{\sin x} \\ \frac{1}{(1-y)}y\text{'}=e^{\sin x} 1-y\ne 0 \\ \frac{1}{(1-y)}dy=e^{\sin x}dx \\ \int \frac{1}{(1-y)}dy=\int e^{\sin x}dx \end{gathered}$$

Kan du fortsätta?

Jag tror det behövs en annan lösning. $\int e^{\sin \left(x\right)}$är inte beräkningar man sysslar med i matte 5. Har du skrivit av uppgiften rätt?

oneplusone2 skrev:

oneplusone2 skrev:

$$\begin{gathered} y\text{'}+e^{\sin x}y=e^{\sin x} \\ y\text{'}=e^{\sin x}-e^{\sin x}y \\ y\text{'}=(1-y)e^{\sin x} \\ \frac{1}{(1-y)}y\text{'}=e^{\sin x} 1-y\ne 0 \\ \frac{1}{(1-y)}dy=e^{\sin x}dx \\ \int \frac{1}{(1-y)}dy=\int e^{\sin x}dx \end{gathered}$$

Kan du fortsätta?

Jag tror det behövs en annan lösning. $\int e^{\sin \left(x\right)}$är inte beräkningar man sysslar med i matte 5. Har du skrivit av uppgiften rätt?

ojjjdå har skrivit fel det ska inte va matte 5

vill du lägga in en bild på den exakta uppgiften?

oneplusone2 skrev:

vill du lägga in en bild på den exakta uppgiften?

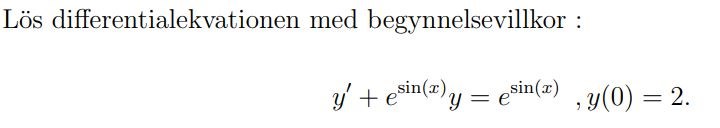
Vad är det för kurs och vilka metoder har ni jobbat med?

Micimacko skrev:

Vad är det för kurs och vilka metoder har ni jobbat med?

Analys 2, vi har gått genom metoden där man multiplicerar med e^x (vet ej vad den metoden heter), men jag förstår ändå inte.

Tror metoden du menar är att hitta en integrerande faktor. Men det går inte här. Och antagligen ingen annan metod som hör hemma i en sån kurs heller. Är det någon a-uppgift eller kan läraren /boken ha skrivit fel?

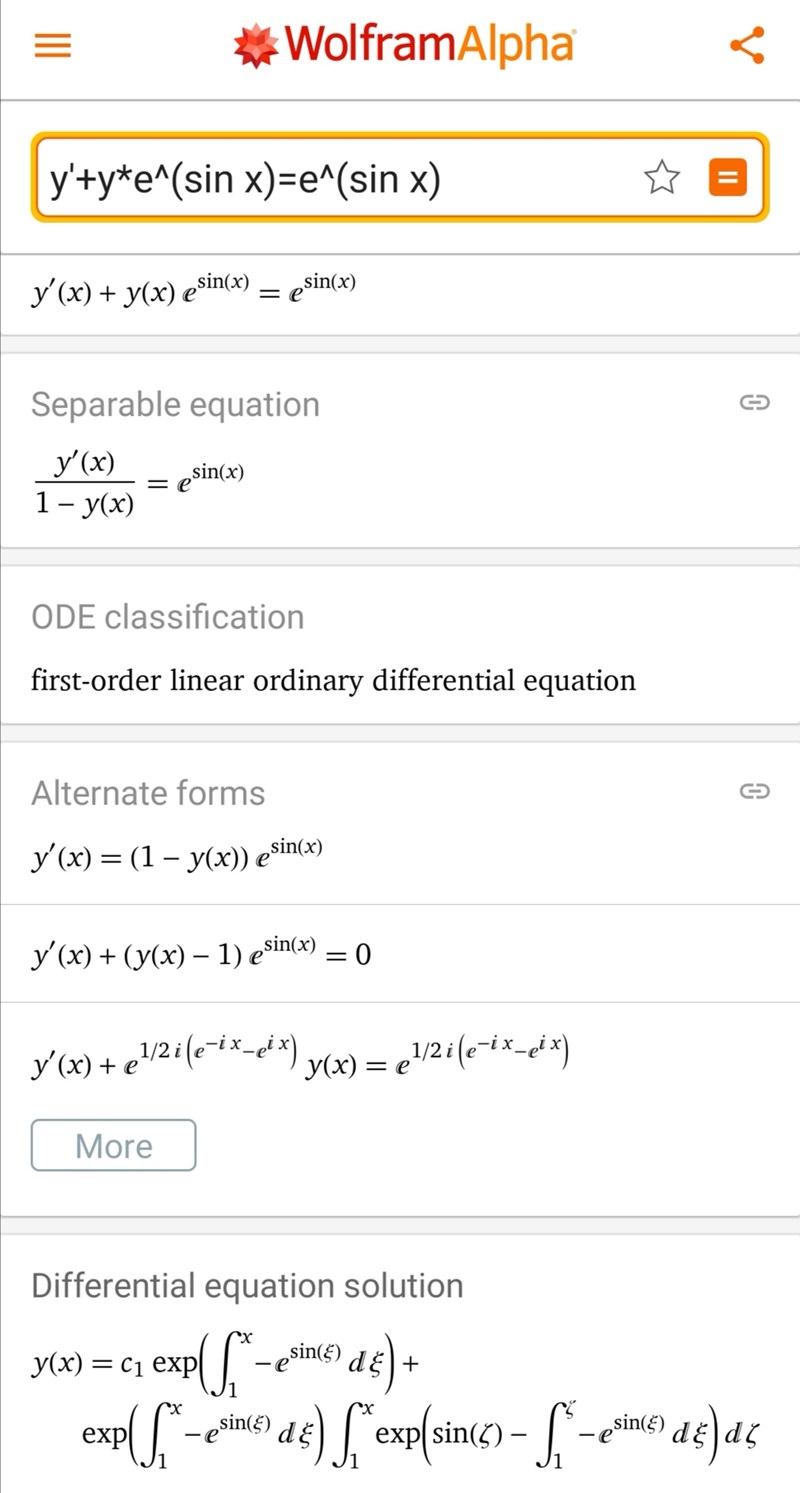
Ingen A-uppgift. Det är en uppgift som alla ska kunna lösa. ska kolla med läraren om det finns någon enkel metod som man borde använda

Den gick att lösa med integrerande faktor, men det blir inget fint svar. Strunta i att räkna ut vad integralen blir och döp den bara till någon bokstav istället och räkna vidare.

Micimacko skrev:

Den gick att lösa med integrerande faktor, men det blir inget fint svar. Strunta i att räkna ut vad integralen blir och döp den bara till någon bokstav istället och räkna vidare.

posta gärna hur du gjorde.

Micimacko skrev:

Den gick att lösa med integrerande faktor

Kan du visa hur du gjorde?

Jag gjorde såhär, om det ens är rätt.

Jag kom så här långt men inte längre.

$$\begin{gathered} \left(y{e}^u\right)\text{'}=e^u{e}^{\sin x} \\ u\text{'}=e^{\sin x} \\ \left(y{e}^u\right)\text{'}=e^u{e}^{\sin x}=e^{u}u\text{'}=\left(e^u\right)\text{'} \\ \left(y{e}^u\right)\text{'}=\left(e^u\right)\text{'} \\ y{e}^u=e^u+c \\ y=1+c{e}^{-u} \end{gathered}$$

Det var en smidigare lösning än min 😅 Jag hade aldrig löst den utan wolframs förslag så jag var väl för inställd på att komma dit.. Bara sätta in u och bestämma nytt c ju.

oneplusone2 skrev:

$e^{u}u\text{'}=\left(e^u\right)\text{'}$

kan du förklara det här steget

Har aldrig använt en definitiv integral för att representera en primitiv, men det kan man kanske. Analysens huvudsats helt enkelt.

$$\begin{gathered} y=1+c{e^{-{\int }_0^{x}e}}^{\sin t_{dt}} \\ y\left(0\right)=2 \\ 2=1+c{e^{-{\int }_0^{0}e}}^{\sin t_{dt}}=1+c{e}^0 \\ 2=1+c \\ c=1 \\ ⋮ \\ y=1+e^{-u} \end{gathered}$$

BabySoda skrev:

oneplusone2 skrev:

$e^{u}u\text{'}=\left(e^u\right)\text{'}$

kan du förklara det här steget

Deriverat med kedjeregeln

oneplusone2 skrev:

Har aldrig använt en definitiv integral för att representera en primitiv, men det kan man kanske.

$$\begin{gathered} y=1+c{e^{-{\int }_0^{t}e}}^{\sin x} \\ y\left(0\right)=2 \\ 2=1+c{e^{-{\int }_0^{0}e}}^{\sin x}=1+c{e}^0 \\ 2=1+c \\ c=-1 \\ y=1-e^{-u} \end{gathered}$$

Här har du y(t) istället för y(x), ser lite konstigt ut. Och jag tycker att 1+1=2 ;)

Micimacko skrev:

BabySoda skrev:

Visa föregående citat

oneplusone2 skrev:

$e^{u}u\text{'}=\left(e^u\right)\text{'}$

kan du förklara det här steget

Deriverat med kedjeregeln

ska det inte vara så här

$$\begin{gathered} \int \left(y{e}^u\right)\text{'}=\int e^{u}u\text{'} \\ -> \\ y{e}^u=\int e^{u}u\text{'} \end{gathered}$$

Micimacko skrev:

oneplusone2 skrev:

Har aldrig använt en definitiv integral för att representera en primitiv, men det kan man kanske.

$$\begin{gathered} y=1+c{e^{-{\int }_0^{t}e}}^{\sin x} \\ y\left(0\right)=2 \\ 2=1+c{e^{-{\int }_0^{0}e}}^{\sin x}=1+c{e}^0 \\ 2=1+c \\ c=-1 \\ y=1-e^{-u} \end{gathered}$$

Här har du y(t) istället för y(x), ser lite konstigt ut. Och jag tycker att 1+1=2 ;)

Fixade till c.

Nu hänger inte jag med alls kan någon snälla förklara

BabySoda skrev:

Micimacko skrev:

Visa föregående citat

BabySoda skrev:

oneplusone2 skrev:

$e^{u}u\text{'}=\left(e^u\right)\text{'}$

kan du förklara det här steget

Deriverat med kedjeregeln

ska det inte vara så här

$$\begin{gathered} \int \left(y{e}^u\right)\text{'}=\int e^{u}u\text{'} \\ -> \\ y{e}^u=\int e^{u}u\text{'} \end{gathered}$$

Jo, och den integralen till höger kan du räkna ut med variabelbytet t=u, för dt=u'dx, så det blir bara e^t kvar att integrera.

Micimacko skrev:

BabySoda skrev:

Visa föregående citat

Micimacko skrev:

BabySoda skrev:

Visa föregående citat

oneplusone2 skrev:

$e^{u}u\text{'}=\left(e^u\right)\text{'}$

kan du förklara det här steget

Deriverat med kedjeregeln

ska det inte vara så här

$$\begin{gathered} \int \left(y{e}^u\right)\text{'}=\int e^{u}u\text{'} \\ -> \\ y{e}^u=\int e^{u}u\text{'} \end{gathered}$$

Jo, och den integralen till höger kan du räkna ut med variabelbytet t=u, för dt=u'dx, så det blir bara e^t kvar att integrera.

ok, nu är jag med.

Kan man kontrollera svaret på något sätt?

Stoppa in det i ekvationen

BabySoda skrev:

Micimacko skrev:

Vad är det för kurs och vilka metoder har ni jobbat med?

Analys 2, vi har gått genom metoden där man multiplicerar med e^x (vet ej vad den metoden heter), men jag förstår ändå inte.

BabySoda, om du läser matte på universitetsnivå skall du lägga dina trådar på Matematik/Universitet, inte Ma5. Om du lägger frågan på Ma5 så måste vi fundera på hur man skall kunna lösa uppgiften med de verktyg man har tillgängliga på Ma5-nivå. Om du lägger frågan på universitesnivå har vi tillgång till hela verktygslådan. Jag flyttar alla dina trådar till rätt nivå. /moderator

ber om ursäkt, som jag sa i min andra post så har jag lagt de fel och märkte det för sent.