Forumutmaning - Max en rad per inlägg!
De flesta firar nog sommarlov och en del har tagit studenten, varför vi tar en uppgift från Studentexamen VT 1902, 123 år senare.
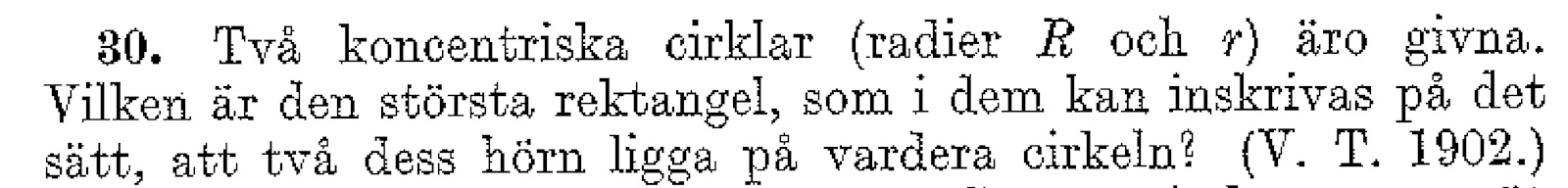
Jag inleder med en skiss:
Rad 1: Vi kan utan inskränkning antaga ovanstånde orientering pga av symmetriskäl och rotationssymmetri. Vidare är det klart att AD skall ligga till vänster om O för maximal area. O = origo. (Med "största rektangel" menas nog "den rektangel med maximal area".)
Om hörnet A ges x-koordinaten -x, så bör A, C och D-koordinaterna bli som följer nedan.

Jan Ragnar skrev:Om hörnet A ges x-koordinaten -x, så bör A, C och D-koordinaterna bli som följer nedan.
Kanske några linjer för att förklara?
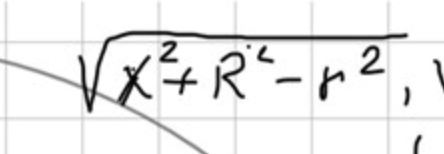
Själv tänkte jag mig en vinkel a mellan "x-axeln" och OC. Rsin(a) kan sedan ersättas med t.ex. t och det blir en ekvation in t. Din kan vara kortare (=bättre).
Trigonometri kan nog vara lika bra eller bättre.
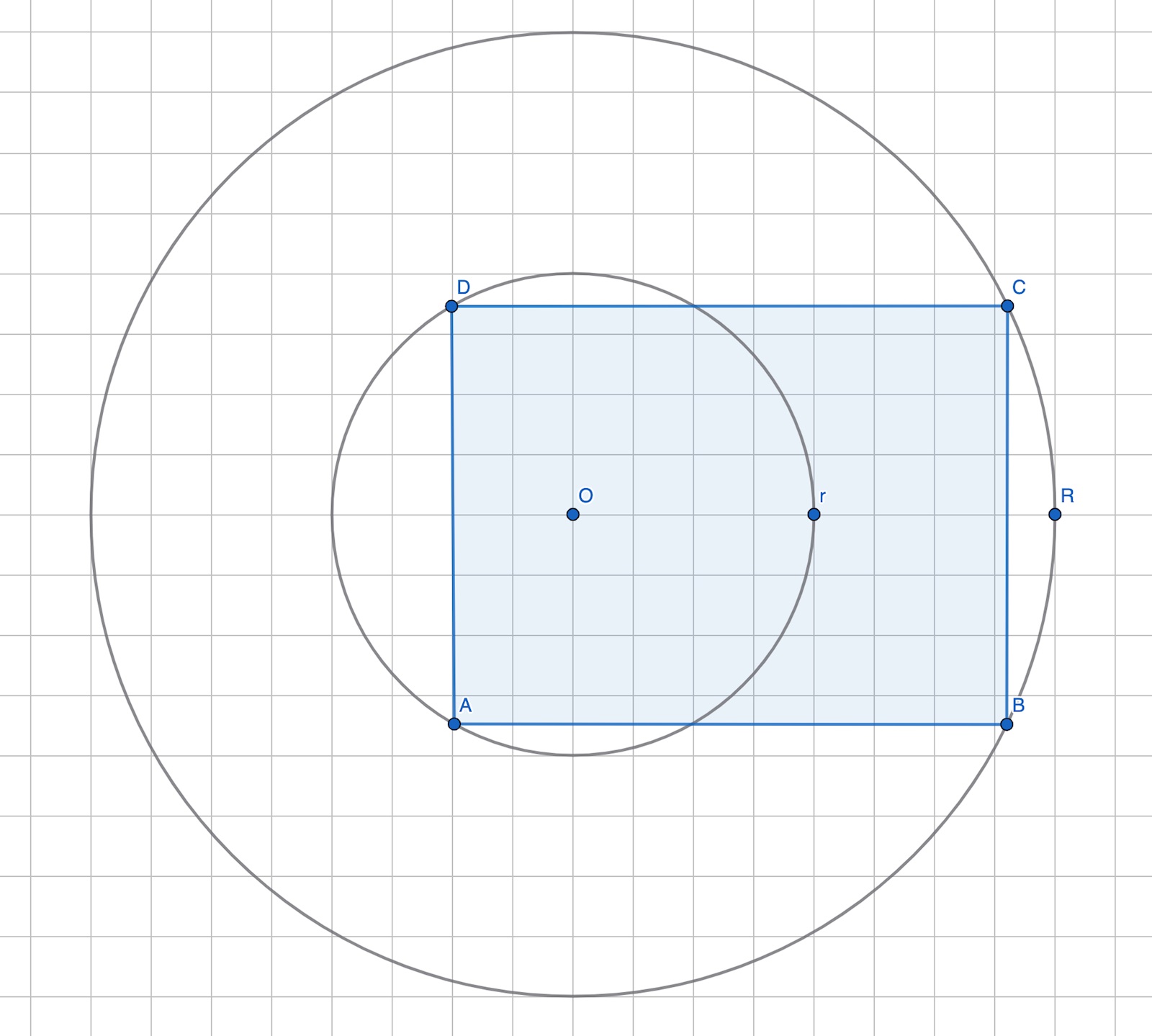
Hörnet C’s x-koordinat är √(R2 -y2) = √(R2-(r2-x2)) = √(x2+R2-r2)). (Orkar inte justera kvadratpotenserna.)
Jan Ragnar skrev:Trigonometri kan nog vara lika bra eller bättre.
Hörnet C’s x-koordinat är √(R2 -y2) = √(R2-(r2-x2)) = √(x2+R2-r2)). (Orkar inte justera kvadratpotenserna.)
Arean är då
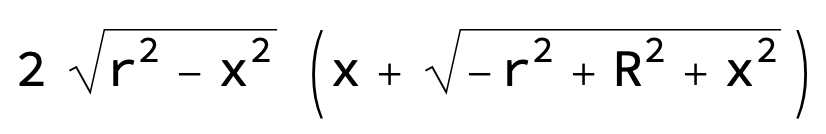
som inte är så svår att derivera. Med trigonometri får jag
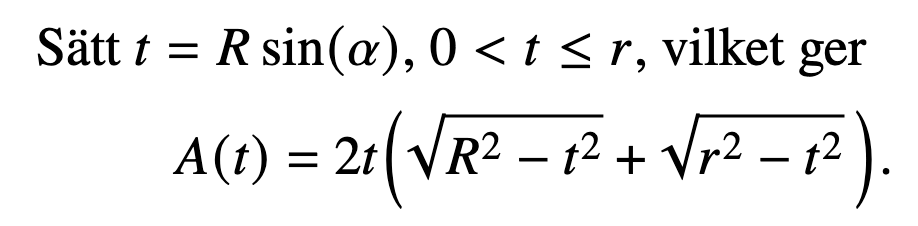
vilket är samma sak som din om man gör en lämplig transformation.
Deriverar man areafunktionen A(x) ovan och söker nollställe för A’(x) får man att maximum inträffar för x = r2/√(r2+R2).
Jan Ragnar skrev:Deriverar man areafunktionen A(x) ovan och söker nollställe för A’(x) får man att maximum inträffar för x = r2/√(r2+R2).
Nja, jag fick det till
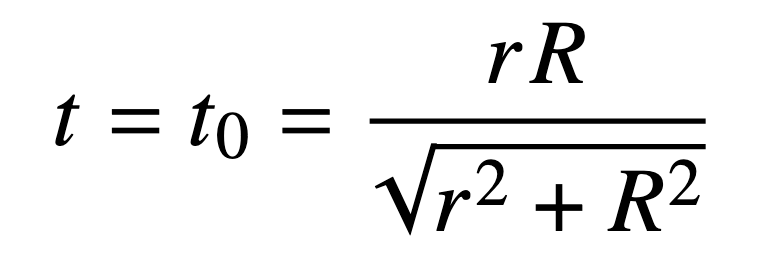
Förhoppningsvis blir slutresultaten desamma. Jag fick Amax = 2•r•R
Jan Ragnar skrev:Förhoppningsvis blir slutresultaten desamma. Jag fick Amax = 2•r•R
Jag med. Ett snyggt svar.
Om båda cirklarna vore lika stora ser man lätt att ytan är A = (R√2)2 = 2R2.
Med olika radier kunde man då ha gissat på 2rR.
Jan Ragnar skrev:Om båda cirklarna vore lika stora ser man lätt att ytan är A = (R√2)2 = 2R2.
Med olika radier kunde man då ha gissat på 2rR.
Att just kvadraten är en optimala rektangeln för en cirkel är väl ett vanligt problem i gymnasieböckerna. Jag tror inte många inser att så är fallet, utan sedvanlig max/min-räkning. Men mycket talar för kvadraten... :)


