Fråga 6 2012
Jag fattar varför A är rätt, för där möts en vänstra källans vågdal med den högra källans vågtopp. Men även C ska vara rätt. Kan någon förklara så jag fattar varför det är så?
Vid C är vågorna från både den vänstra och högra vågkällan mitt emellan en vågtopp och en vågdal. Amplituden för båda vågorna är alltså noll där.
Yes, det är sant. Mycket enklare också när man kollar på ett diagram. Känns som längesedan jag kollade på ett sådant. Men då är det mycket riktigt ingen amplitud från varken den högra- eller vänstrakällan så tillsammans blir naturligtvis amplituden 0. Räknas även detta då som nod? Antar det pga svaret i facit, men dubbelkollar gärna med er.
Ja, det stämmer.
Det är givet att avståndet mellan källorna är fyra våglängder. I punkt D är avståndet till den vänstra källan 2,5 λ och till den högre 1,5 λ, så ∆sD = λ och där är det konstruktiv interferens.
Vid punkt C är väglängdsskillnaden ∆sC = λ/2 och där är det destruktiv interferens, utsläckning.
Det är lättare att rita in linjerna för konstruktiv interferens, antinoderna: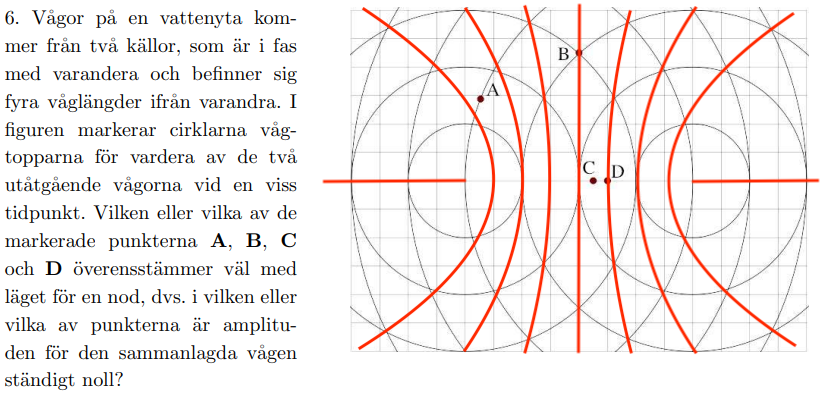
Nodlinjerna ligger mellan dessa röda linjerna, så rätt svar är "A och C".
Arbetsmyran skrev:Men då är det mycket riktigt ingen amplitud från varken den högra- eller vänstrakällan så tillsammans blir naturligtvis amplituden 0.
Det stämmer inte. Yngve skrev fel.
Om endast en källa är på, är det rörelse överallt, amplituden är stor överallt.
Kolla denna interaktiva simulering som kan ge en bättre förståelse än dessa statiska figurer:
https://phet.colorado.edu/sims/html/wave-interference/latest/wave-interference_sv.html
Pieter Kuiper skrev:
Det stämmer inte. Yngve skrev fel.
Om endast en källa är på, är det rörelse överallt, amplituden är stor överallt.
Du har rätt, jag tänkte fel.
Pieter Kuiper skrev:Arbetsmyran skrev:Men då är det mycket riktigt ingen amplitud från varken den högra- eller vänstrakällan så tillsammans blir naturligtvis amplituden 0.
Det stämmer inte. Yngve skrev fel.
Om endast en källa är på, är det rörelse överallt, amplituden är stor överallt.
Kolla denna interaktiva simulering som kan ge en bättre förståelse än dessa statiska figurer:
https://phet.colorado.edu/sims/html/wave-interference/latest/wave-interference_sv.html
Om jag förstått det rätt, så menar du att det inte finns en punkt där en våg alltid har amplitud 0, eftersom vågen hela tiden utbreder sig. Så det enda sättet det kan bli noll i en punkt är genom destruktiv interferens, vilket är fallet i C eftersom vägskillnaden är ett "halvantal" (inte pga att det eventuellt hade kunnat vara två noder där redan från början, som det kanske inte nödvändigtvis behöver vara). Är det korrekt uppfattat?
Arbetsmyran skrev:Om jag förstått det rätt, så menar du att det inte finns en punkt där en våg alltid har amplitud 0, eftersom vågen hela tiden utbreder sig. Så det enda sättet det kan bli noll i en punkt är genom destruktiv interferens, vilket är fallet i C eftersom vägskillnaden är ett "halvantal" (inte pga att det eventuellt hade kunnat vara två noder där redan från början, som det kanske inte nödvändigtvis behöver vara). Är det korrekt uppfattat?
För en fortskridande våg från en källa finns rörelse överallt, ja.
Med två källor kan det uppstå interferens. Förutom att "leka" med simuleringen som jag länkade kan det vara bra att titta på denna film av Veritassium:
https://youtu.be/Iuv6hY6zsd0?si=SWwJy-SLaERjvBmZ&t=269
